题目内容
函数y=x+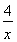 (x≠0)的值域是________.
(x≠0)的值域是________.
(-∞,-4]∪[4,+∞)
【解析】当x>0时,y=x+ ≥2
≥2 =4,当x<0时,y=x+
=4,当x<0时,y=x+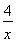 =-
=-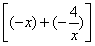 ≤-2
≤-2 =-4.
=-4.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
函数y=x+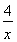 (x≠0)的值域是________.
(x≠0)的值域是________.
(-∞,-4]∪[4,+∞)
【解析】当x>0时,y=x+ ≥2
≥2 =4,当x<0时,y=x+
=4,当x<0时,y=x+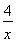 =-
=-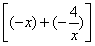 ≤-2
≤-2 =-4.
=-4.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案