题目内容
设a+b=2,b>0,则当a=________时,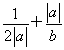 取得最小值.
取得最小值.
-2
【解析】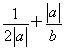 =
=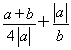 =
=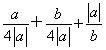 ≥-
≥-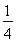 +2
+2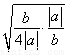 =
=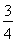 ,当且仅当
,当且仅当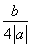 =
=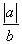 且a<0取等号,即a=-2,b=4.
且a<0取等号,即a=-2,b=4.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
设a+b=2,b>0,则当a=________时,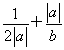 取得最小值.
取得最小值.
-2
【解析】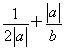 =
=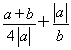 =
=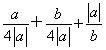 ≥-
≥-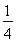 +2
+2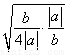 =
=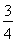 ,当且仅当
,当且仅当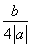 =
=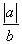 且a<0取等号,即a=-2,b=4.
且a<0取等号,即a=-2,b=4.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案