题目内容
【题目】已知函数f(x)=|2x﹣1|﹣2|x﹣1|.
(I)作出函数f(x)的图象;
(Ⅱ)若不等式 ![]() ≤f(x)有解,求实数a的取值范围.
≤f(x)有解,求实数a的取值范围.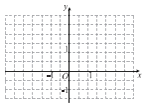
【答案】解:(Ⅰ)令2x﹣1=0,得x= ![]() ,
,
令x﹣1=0,得x=1;
当x< ![]() 时,函数f(x)=|2x﹣1|﹣2|x﹣1|=﹣(2x﹣1)+2(x﹣1)=﹣1;
时,函数f(x)=|2x﹣1|﹣2|x﹣1|=﹣(2x﹣1)+2(x﹣1)=﹣1;
当 ![]() ≤x≤1时,函数f(x)=|2x﹣1|﹣2|x﹣1|=(2x﹣1)+2(x﹣1)=4x﹣3;
≤x≤1时,函数f(x)=|2x﹣1|﹣2|x﹣1|=(2x﹣1)+2(x﹣1)=4x﹣3;
当x>1时,函数f(x)=|2x﹣1|﹣2|x﹣1|=(2x﹣1)﹣2(x﹣1)=1;
∴f(x)= 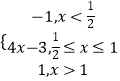 ,
,
作出函数f(x)的图象,如图所示;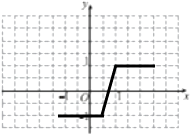
(Ⅱ)由函数f(x)的图象知,f(x)的最大值是1,
所以不等式 ![]() ≤f(x)有解,等价于
≤f(x)有解,等价于 ![]() ≤1有解,
≤1有解,
不等式 ![]() ≤1可化为
≤1可化为 ![]() ﹣1≤0
﹣1≤0
(2a﹣1)(a﹣1)≥0(a≠1),解得a≤ ![]() 或a>1,
或a>1,
所以实数a的取值范围是(﹣∞, ![]() ]∪(1,+∞)
]∪(1,+∞)
【解析】(Ⅰ)去掉绝对值,化简函数f(x),作出函数f(x)的图象即可;(Ⅱ)由函数f(x)的图象知函数的最大值是1,问题等价于 ![]() ≤1有解,
≤1有解,
求出解集即可.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目