��Ŀ����
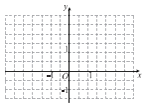
����Ŀ����֪������ ![]() �Ľ���F1����Բ
�Ľ���F1����Բ ![]() ��һ�������غϣ���������x��Ľ���ΪF1 �� ������C�Ľ���ΪA��B���ҵ�A����F1 �� F2�ľ���֮��Ϊ4��
��һ�������غϣ���������x��Ľ���ΪF1 �� ������C�Ľ���ΪA��B���ҵ�A����F1 �� F2�ľ���֮��Ϊ4��
��������ԲC�ķ��̣�
����������ԭ����б�ʴ��ڵ�ֱ��l����ԲC�ڵ�G��H���ҡ�OGH�����Ϊ1���߶�GH���е�ΪP����x�����Ƿ���ڹ���ԭ��ԳƵ���������M��N��ʹ��ֱ��PM��PN��б��֮��Ϊ��ֵ�������ڣ����������M��N������Ͷ�ֵ�Ĵ�С���������ڣ���˵�����ɣ�
���𰸡��⣺������������ ![]() �Ľ���
�Ľ��� ![]() ����Բ
����Բ ![]() ��һ�������غϣ�
��һ�������غϣ�
�� ![]() ��
��
�֡������ߦ�������x��Ľ���ΪF1�� ![]() ��0�����ҵ�A����F1 �� F2�ľ���֮��Ϊ4��������Բ�ϵĶ���֪2a=4��
��0�����ҵ�A����F1 �� F2�ľ���֮��Ϊ4��������Բ�ϵĶ���֪2a=4��
���a=2����b2=a2��c2=4��3=1��
����ԲC�ķ���Ϊ ![]() ��
��
������ֱ��l��y=kx+m��m��0����G��x1 �� y1����H��x2 �� y2����
���� 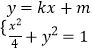 ���ã�1+4k2��x2+8kmx+4m2��4=0��
���ã�1+4k2��x2+8kmx+4m2��4=0��
���б�ʽ����ϵ����Ĺ�ϵ֪��=��8km��2��4��1+4k2����4m2��4��=16��4k2+1��m2����0��![]() �������ҳ���ʽ֪حGHح=
�������ҳ���ʽ֪حGHح= ![]() حx1��x2ح=
حx1��x2ح= ![]()
![]() =
= ![]() ��
��
�ָ��ݵ㵽ֱ�ߵľ��빫ʽ֪ԭ��O��ֱ��y=kx+m�ľ���Ϊ ![]()
���ǡ�OGH�����Ϊ ![]() �������ã�1+4k2��2m2��2=0��
�������ã�1+4k2��2m2��2=0��
��1+4k2��2m2=0��
���߶�GH���е� ![]() ����
���� ![]() ��
��
����������������Ķ���M��N��������M��s��0����N����s��0����s��0����ֱ��PM��PN��б��֮��Ϊt��
���� 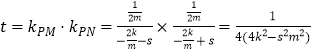 ��������
�������� ![]() �ڣ�
�ڣ�
���ٴ���ڣ��� ![]() ��
��
��ֱ��l�������Կɵ� 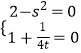 �����
�����  ��
��
���Ǵ��������� ![]() ��ʹ��ֱ��PM��PN��б��֮��Ϊ��ֵ����ֵΪ
��ʹ��ֱ��PM��PN��б��֮��Ϊ��ֵ����ֵΪ ![]() ��
��
�������������������߷��̣����c= ![]() ��������Բ�Ķ��壬���2a=4���������a����b2=a2��c2=4��3=1�����������ԲC�ķ��̣�������ֱ��l�ķ��̣�������Բ���̣�����Τ�ﶨ�����ҳ���ʽ���حGHح�����ɵ㵽ֱ�ߵľ��빫ʽ�������ε������ʽ��á�OGH����������1+4k2��2m2=0�������е����깫ʽ��ֱ�ߵ�б�ʹ�ʽ���s��t��ֵ��ʹ��ֱ��PM��PN��б��֮��Ϊ��ֵ��
��������Բ�Ķ��壬���2a=4���������a����b2=a2��c2=4��3=1�����������ԲC�ķ��̣�������ֱ��l�ķ��̣�������Բ���̣�����Τ�ﶨ�����ҳ���ʽ���حGHح�����ɵ㵽ֱ�ߵľ��빫ʽ�������ε������ʽ��á�OGH����������1+4k2��2m2=0�������е����깫ʽ��ֱ�ߵ�б�ʹ�ʽ���s��t��ֵ��ʹ��ֱ��PM��PN��б��֮��Ϊ��ֵ��

 ����ʦ���һ��һ��ϵ�д�
����ʦ���һ��һ��ϵ�д�