Question

19．已知三棱锥P-ABC中，PA=PB=PC=4，且PA、PB、PC两两垂直，若此三棱锥的四个顶点都在球面上，则这个球的体积为32$\sqrt{3}$πcm³．

Answer 1

分析 设过A，B，C的截面圆的圆心为O′，半径为r，球心O到该截面的距离为d，利用PA，PB，PC两两垂直，O′为△ABC的中心，求出截面圆的半径，通过球的半径截面圆的半径球心与截面的距离，求出球的半径，即可求出球的体积．

解答 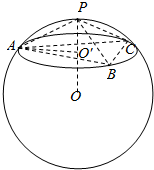解：如图，设过A，B，C的截面圆的圆心为O′，半径为r，球心O到该截面的距离为d，
∵PA，PB，PC两两垂直，且PA=PB=PC=4，
∴AB=BC=CA=4$\sqrt{2}$，且O′为△ABC的中心，
于是$\frac{4\sqrt{2}}{sin60°}$=2r，得r=$\frac{4\sqrt{6}}{3}$，
又PO′=$\sqrt{16-{r}^{2}}$=$\frac{4\sqrt{3}}{3}$．
OO′=R-$\frac{4\sqrt{3}}{3}$=d=$\sqrt{{R}^{2}-{r}^{2}}$，解得R=2$\sqrt{3}$，
故V_球=$\frac{4}{3}$πR³=32$\sqrt{3}$π．
故答案为：32$\sqrt{3}$π．

点评 本题是中档题，考查球的体积的求法，球的截面圆的有关性质，考查空间想象能力，计算能力．