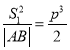题目内容
【题目】如图1,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的点,
上的点,![]() ,
,![]() 为
为![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起到
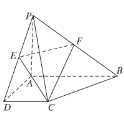
折起到![]() 的位置,使得
的位置,使得![]() ,如图2.
,如图2.
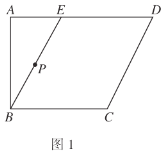
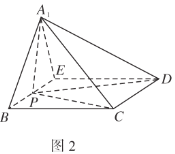
(1)求证:平面![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上,当直线
上,当直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)计算出![]() 、
、![]() 、
、![]() 的长,利用勾股定理证明出
的长,利用勾股定理证明出![]() ,
,![]() ,利用线面垂直的判定定理可证明出
,利用线面垂直的判定定理可证明出![]() 平面
平面![]() ,再利用面面垂直的判定定理可证得结论;
,再利用面面垂直的判定定理可证得结论;
(2)以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴建立空间直角坐标系,设点
轴建立空间直角坐标系,设点![]() ,求出平面
,求出平面![]() 的一个法向量的坐标,利用空间向量法结合线面角的正弦值可求得
的一个法向量的坐标,利用空间向量法结合线面角的正弦值可求得![]() 的值,然后利用空间向量法可求得二面角
的值,然后利用空间向量法可求得二面角![]() 的余弦值.
的余弦值.
(1)因为![]() ,
,![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,所以
,所以![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ;
;
(2)以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴建立空间直角坐标系如图所示,
轴建立空间直角坐标系如图所示,
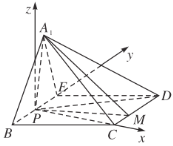
则![]() 、
、![]() 、
、![]() ,设
,设![]() ,其中
,其中![]() ,
,
则![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由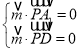 ,得
,得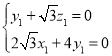 ,
,
令![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() ,
,
所以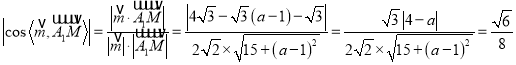 ,
,
化简得![]() ,解得
,解得![]() 或
或![]() (舍),
(舍),
所以![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由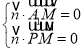 ,得
,得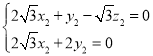 ,
,
令![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() ,
,
所以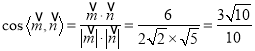 .
.
由图可知二面角![]() 为锐二面角,
为锐二面角,
所以当直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,二面角
时,二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】为调查某地区被隔离者是否需要社区非医护人员提供帮助,用简单随机抽样方法从该地区调查了500位被隔离者,结果如下:
性别 是否需要 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(1)估计该地区被隔离者中,需要社区非医护人员提供帮助的被隔离者的比例;
(2)能否有99%的把握认为该地区的被隔离者是否需要社区非医护人员提供帮助与性别有关?