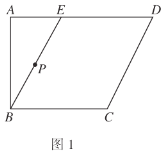
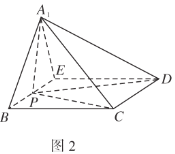
题目内容
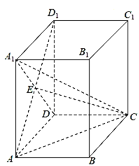
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若存在与函数![]() ,
,![]() 的图象都相切的直线,求
的图象都相切的直线,求![]() 的取值范围.
的取值范围.
【答案】(1)答案见解析;(2)![]() .
.
【解析】
(1)求![]() 的定义域,导数,利用二次函数的性质分类讨论导数的正负,从而求出
的定义域,导数,利用二次函数的性质分类讨论导数的正负,从而求出![]() 的单调性. (2)函数
的单调性. (2)函数![]() 的图象上点
的图象上点![]() 与函数
与函数![]() 的图象上点
的图象上点![]() 处切线相同,利用导数求切线的斜率建立关系式,求出导数和单调区间以及最值,运用单调性计算可求出
处切线相同,利用导数求切线的斜率建立关系式,求出导数和单调区间以及最值,运用单调性计算可求出![]() 的范围.
的范围.
(1)函数![]() 的定义域为
的定义域为![]() ,
,
![]() .
.
![]() ,
,
所以当![]() 即
即![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() ,即
,即![]() 或
或![]() 时,
时,
方程![]() 的根为
的根为![]() ,
,![]() .
.
当![]() 时,有
时,有![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,有
时,有![]() .
.
|
|
|
|
| + | - | + |
| 增 | 减 | 增 |
综上:当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() 在
在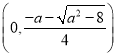 ,
,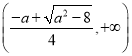 上单调递增,
上单调递增,
在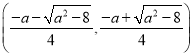 上单调递减.
上单调递减.
(2)设函数![]() 的图象上点
的图象上点![]() 与函数
与函数![]() 的图象上点
的图象上点![]() 处切线相同,
处切线相同,
则![]() ,
,
即![]() ,
,
由![]() 得
得![]() ①
①
由![]() ,
,
得![]() ②
②
由①②得:![]() ,
,
设![]()
问题转化为![]() 在
在![]() 有解,
有解,
则![]() ,
,
不妨设![]() ,
,
则当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
∴![]() 是
是![]() 的最小值.
的最小值.
只需![]() ,即
,即![]() ③
③
而![]() ,故
,故![]() 代入③式,得
代入③式,得
![]() ,
,
令![]() ,易得
,易得![]() ,
,
![]() ,则
,则![]() 在
在![]() 递增.
递增.
故![]() 的解集是(0,1],即
的解集是(0,1],即![]() .
.
由![]() ,得
,得![]() .
.
即实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
【题目】某学校数学建模小组为了研究双层玻璃窗户中每层玻璃厚度![]() (每层玻璃的厚度相同)及两层玻璃间夹空气层厚度
(每层玻璃的厚度相同)及两层玻璃间夹空气层厚度![]() 对保温效果的影响,利用热传导定律得到热传导量
对保温效果的影响,利用热传导定律得到热传导量![]() 满足关系式
满足关系式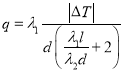 ,其中玻璃的热传导系数
,其中玻璃的热传导系数![]() 焦耳/(厘米·度),不流通、干燥空气的热传导系数
焦耳/(厘米·度),不流通、干燥空气的热传导系数![]() 焦耳/(厘米·度),
焦耳/(厘米·度),![]() 为室内外温度差,
为室内外温度差,![]() 值越小,保温效果越好,现有4种型号的双层玻璃窗户,具体数据如下表:
值越小,保温效果越好,现有4种型号的双层玻璃窗户,具体数据如下表:
型号 | 每层玻璃厚度 | 玻璃间夹空气层厚度 |
| 0.4 | 3 |
| 0.3 | 4 |
| 0.5 | 3 |
| 0.4 | 4 |
则保温效果最好的双层玻璃的型号是( )
A.![]() 型B.
型B.![]() 型C.
型C.![]() 型D.
型D.![]() 型
型