题目内容
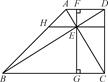
如图,在梯形ABCD中,AD∥BC,AC⊥BD,垂足为E,∠ABC=45°,过E作AD的垂线交AD于F,交BC于G,过E作AD的平行线交AB于H.求证:FG2=AF·DF+BG·CG+AH·BH.

见解析
因为AC⊥BD,故△AED、△BEC都是直角三角形.
又EF⊥AD,EG⊥BC,
由射影定理可知AF·DF=EF2,
BG·CG=EG2.
又FG2=(FE+EG)2=FE2+EG2+2FE·EG=AF·DF+BG·CG+2FE·EG,∠ABC=45°,如图,过点H、A分别作直线HM、AN与BC垂直,易知,AH= FE,BH=
FE,BH= EG,故AH·BH=2EF·EG.所以
EG,故AH·BH=2EF·EG.所以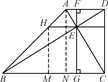
FG2=AF·DF+BG·CG+2FE·EG=AF·DF+BG·CG+AH·BH.
又EF⊥AD,EG⊥BC,
由射影定理可知AF·DF=EF2,
BG·CG=EG2.
又FG2=(FE+EG)2=FE2+EG2+2FE·EG=AF·DF+BG·CG+2FE·EG,∠ABC=45°,如图,过点H、A分别作直线HM、AN与BC垂直,易知,AH=
 FE,BH=
FE,BH= EG,故AH·BH=2EF·EG.所以
EG,故AH·BH=2EF·EG.所以
FG2=AF·DF+BG·CG+2FE·EG=AF·DF+BG·CG+AH·BH.

练习册系列答案
 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目

 是⊙
是⊙ 的直径,
的直径, 是弧
是弧 的中点,
的中点, ⊥
⊥ ,
, .
.
 =
= ;
; =4,⊙
=4,⊙ 的长.
的长. 的圆心
的圆心 的直角边
的直角边 上,该圆与直角边
上,该圆与直角边 相切,与斜边
相切,与斜边 交于
交于 ,
, ,
, .
.
 的两条弦, AB与CD相交于点E,且
的两条弦, AB与CD相交于点E,且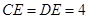 ,
,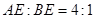 ,则
,则 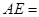 ______;
______;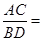 ______.
______.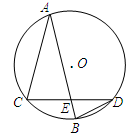
 ,OA=
,OA=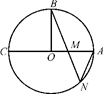
 .
. ,
, ,则CP= .
,则CP= .
 的值为________.
的值为________.