题目内容
如图,在梯形ABCD中,AD∥BC,∠ADC=90°,E是AB边的中点,求证:ED=EC.


见解析
证明:如图,过E点作EF∥BC交DC于点F.在梯形ABCD中,AD∥BC,
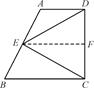
∴AD∥EF∥BC.
∵E是AB的中点,
∴F是DC的中点.
∵∠ADC=90°,
∴∠DFE=90°.
∴EF是DC的垂直平分线,
∴ED=EC.

∴AD∥EF∥BC.
∵E是AB的中点,
∴F是DC的中点.
∵∠ADC=90°,
∴∠DFE=90°.
∴EF是DC的垂直平分线,
∴ED=EC.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目

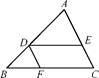
 AD,N是AB的中点,NF⊥CE于F,求证:FN2=EF·FC.
AD,N是AB的中点,NF⊥CE于F,求证:FN2=EF·FC.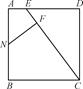
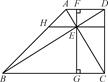


 (2)若AD=2,CD=3.DB=4,求
(2)若AD=2,CD=3.DB=4,求 的值.
的值.
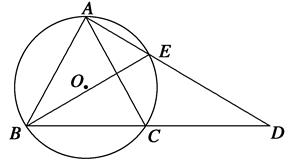
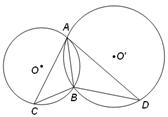
 和
和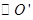 相交于
相交于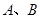 两点,过
两点,过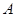 作两圆的切线分别交两圆于
作两圆的切线分别交两圆于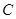 、
、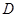 两点,连接
两点,连接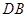 、
、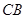 ,已知
,已知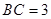 ,
,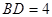 ,则
,则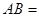 .
.