题目内容
已知等差数列{an}的前n项和Sn,且对于任意的正整数n满足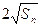
=an+1.
(1)求数列{an}的通项公式;
(2)设bn=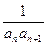
,求数列{bn}的前n项和Bn.
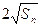=an+1.(1)求数列{an}的通项公式;
(2)设bn=
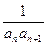,求数列{bn}的前n项和Bn.(1)数列{an}是首项为1公差为2的等差数列.
∴an=1+(n-1)×2=2n-1.
(2) bn=
=
(
-
).
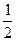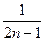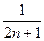∴Bn==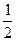(1-).
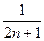∴an=1+(n-1)×2=2n-1.
(2) bn=
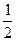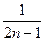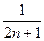=(-).∴Bn==
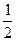(1-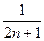).(1)∵对于任意的正整数n,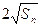=an+1①恒成立,
当n=1时,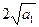
=a1+1,即(
-1)2=0,
∴a1=1.
当n≥2时,有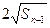
=an-1+1②,
①2-②2得4an=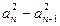
+2an-2an-1,
即(an+an-1)(an-an-1-2)=0.
∵an＞0,∴an+an-1＞0.
∴an-an-1=2.
∴数列{an}是首项为1公差为2的等差数列.
∴an=1+(n-1)×2=2n-1.
(2)∵an=2n-1,
∴bn==(-).
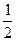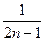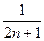∴Bn=b1+b2+…+bn
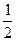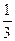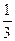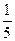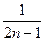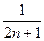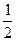=［(1-
)+(-
)+…+(-)］
=(1-).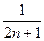
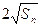=an+1①恒成立,当n=1时,
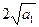=a1+1,即(-1)2=0,∴a1=1.
当n≥2时,有
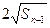=an-1+1②,①2-②2得4an=
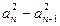+2an-2an-1,即(an+an-1)(an-an-1-2)=0.
∵an＞0,∴an+an-1＞0.
∴an-an-1=2.
∴数列{an}是首项为1公差为2的等差数列.
∴an=1+(n-1)×2=2n-1.
(2)∵an=2n-1,
∴bn=
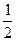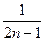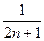=(-).∴Bn=b1+b2+…+bn
=
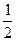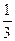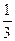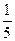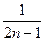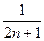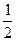［(1-)+(-)+…+(-)］=
(1-).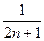
练习册系列答案
相关题目
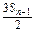总成等差数列.
.
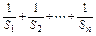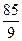,求这5个数.
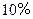，那么从今年起大约几年可使总销售量达到30000台（结果保留到个位）？
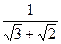，b=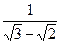
，则a、b的等差中项为（ ）
