题目内容
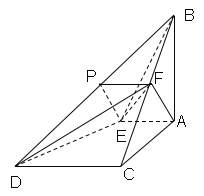
【题目】如图所示，四棱锥B-AEDC中，平面AEDC⊥平面ABC，F为BC的中点，P为BD的中点，且AE//DC，∠ACD=∠BAC=90°，DC=AC=AB=2AE
（1）证明：EP⊥平面BCD；
（2）若DC=2，求三棱锥E-BDF的体积.
【答案】（1）见解析（2）
【解析】试题分析：（1）先根据等腰三角形性质得
，再根据面面垂直性质得
平面
.，即得
，从而可由线面垂直判定定理得
平面
.最后根据平行四边形性质得
即得结论，（2）因为
平面，所以根据锥体体积公式求体积.
试题解析：（（Ⅰ）由题意知
为等腰直角三角形，
而
为
的中点，所以.
又因为平面
平面，且
，
所以平面.
而
平面
，所以.
而
所以平面.
连结
,则
而
所以
是平行四边形,因此
平面.
（Ⅱ）因为平面，所以平面
是三棱锥
的高.
所以
. 于是三棱锥的体积为
练习册系列答案
相关题目
