题目内容
【题目】某公司想了解对某产品投入的宣传费用与该产品的营业额的影响.右图是以往公司对该产品的宣传费用![]() (单位:万元)和产品营业额
(单位:万元)和产品营业额![]() (单位:万元)的统计折线图.
(单位:万元)的统计折线图.

(Ⅰ)根据折线图可以判断,可用线性回归模型拟合宣传费用![]() 与产品营业额
与产品营业额![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(Ⅱ)建立产品营业额![]() 关于宣传费用
关于宣传费用![]() 的回归方程;
的回归方程;
(Ⅲ)若某段时间内产品利润![]() 与宣传费
与宣传费![]() 和营业额
和营业额![]() 的关系为
的关系为![]() 应投入宣传费多少万元才能使利润最大,并求最大利润. (计算结果保留两位小数)
应投入宣传费多少万元才能使利润最大,并求最大利润. (计算结果保留两位小数)
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
参考公式:相关系数 ,回归方程
,回归方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为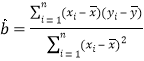 ,
,![]() .
.
【答案】(1)见解析;(2)![]() ;(3)投入宣传费3万元时,可获得最大利润55.4万元.
;(3)投入宣传费3万元时,可获得最大利润55.4万元.
【解析】
(1)根据公式计算![]() 与
与![]() 的相关系数,再根据系数值作出判断,(2)先求均值,再代入公式求
的相关系数,再根据系数值作出判断,(2)先求均值,再代入公式求![]() ,
,![]() ,即得结果,(3)将回归直线方程代入,再根据二次函数性质求最值.
,即得结果,(3)将回归直线方程代入,再根据二次函数性质求最值.
(Ⅰ)由折线图中数据和参考数据得:![]() ,
,![]() ,
,
![]() ,又
,又![]() ,
,
![]() ,∴
,∴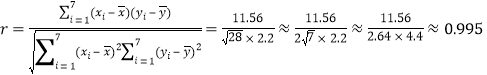 ,
,
因为![]() 与
与![]() 的相关系数近似为
的相关系数近似为![]() ,说明
,说明![]() 与
与![]() 的线性相关程度相当高,从而可以用线性回归模型拟合
的线性相关程度相当高,从而可以用线性回归模型拟合![]() 与
与![]() 的关系.
的关系.
(Ⅱ)又![]() ,∴
,∴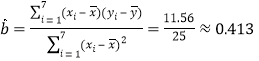 ,
,
∴![]() ,所以
,所以![]() 关于
关于![]() 的回归方程为
的回归方程为![]() .
.
(Ⅲ)故![]() ,故当
,故当![]() 时,
时,![]() .所以投入宣传费3万元时,可获得最大利润55.4万元.
.所以投入宣传费3万元时,可获得最大利润55.4万元.

【题目】进入冬天,大气流动性变差,容易形成雾握天气,从而影响空气质量.某城市环保部门试图探究车流量与空气质量的相关性,以确定是否对车辆实施限行.为此,环保部门采集到该城市过去一周内某时段车流量与空气质量指数的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
车流量(x万辆) | 10 | 9 | 9.5 | 10.5 | 11 | 8 | 8.5 |
空气质量指数y | 78 | 76 | 77 | 79 | 80 | 73 | 75 |
(1)根据表中周一到周五的数据,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2,则认为得到的线性回归方程是可靠的.请根据周六和周日数据,判定所得的线性回归方程是否可靠?
附:回归方程![]() 中斜率和截距最小二乘估计公式分别为:
中斜率和截距最小二乘估计公式分别为:
 其中:
其中:![]()
![]()

