题目内容
【题目】设椭圆![]() (
(![]() )的右焦点为
)的右焦点为![]() ,右顶点为
,右顶点为![]() ,已知
,已知![]() ,其中
,其中![]() 为原点,
为原点,![]() 为椭圆的离心率.
为椭圆的离心率.
(Ⅰ)求椭圆的方程;
(Ⅱ)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线的
,求直线的![]() 斜率.
斜率.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(Ⅰ)求椭圆标准方程,只需确定![]() ,由
,由![]() ,得
,得![]() ,再利用
,再利用![]() ,可解得
,可解得![]() ,
,![]() ;
;
(Ⅱ)先化简条件:![]()
![]()
![]() ,即M再OA中垂线上,
,即M再OA中垂线上,![]() .设直线
.设直线![]() 方程为
方程为![]() ,点
,点![]() 可求;根据
可求;根据![]() ,求点H,由点斜式得到直线MH方程,联立直线
,求点H,由点斜式得到直线MH方程,联立直线![]() 和直线MH方程,求得
和直线MH方程,求得![]() 表达式,列等量关系解出直线斜率.
表达式,列等量关系解出直线斜率.
解:(Ⅰ)设![]() ,由
,由![]() ,即
,即![]() ,
,
可得![]() ,又
,又![]() ,
,
所以![]() ,因此
,因此![]() ,所以椭圆的方程为
,所以椭圆的方程为![]() .
.
(Ⅱ)设![]() ,直线的斜率为
,直线的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
由方程组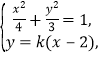 消去
消去![]() ,整理得
,整理得![]() ,
,
解得![]() 或
或![]() ,
,
由题意得![]() ,从而
,从而![]() ,
,
设![]() ,由(1)知
,由(1)知![]() , 有
, 有![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,
,
所以![]() ,解得
,解得![]() ,
,
因此直线![]() 的方程为
的方程为![]() ,
,
设![]() ,由方程组
,由方程组 消去
消去![]() ,得
,得![]() ,
,
在![]() 中,
中,![]()
![]()
![]() ,
,
即![]() ,化简得
,化简得![]() ,即
,即![]() ,
,
解得![]() 或
或![]() ,
,
所以直线![]() 的斜率为
的斜率为![]() 或
或![]() .
.

【题目】目前,学案导学模式已经成为教学中不可或缺的一部分,为了了解学案的合理使用是否对学生的期末复习有着重要的影响,我校随机抽取100名学生,对学习成绩和学案使用程度进行了调查,统计数据如表所示:
善于使用学案 | 不善于使用学案 | 总计 | |
学习成绩优秀 | 40 | ||
学习成绩一般 | 30 | ||
总计 | 100 |
参考公式: ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
参考数据:
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
已知随机抽查这100名学生中的一名学生,抽到善于使用学案的学生概率是0.6.
(1)请将上表补充完整(不用写计算过程);
(2)试运用独立性检验的思想方法分析:有多大的把握认为学生的学习成绩与对待学案的使用态度有关?
(3)利用分层抽样的方法从善于使用学案的同学中随机抽取6人,从这6人中抽出3人继续调查,设抽出学习成绩优秀的人数为X,求X的分布列和数学期望.