题目内容
设正实数x,y满足条件
,则lg(x2y)的最大值为______.
|
正实数x,y满足条件
,
即
,
令a=lgx,b=lgy,
则
,
满足条件的可行域如下图所示:
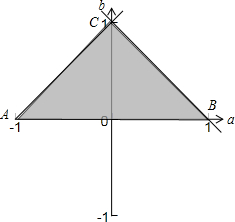
当a=-1,b=0时,lg(x2y)=2lgx+lgy=2a+b=-2
当a=1,b=0时,lg(x2y)=2lgx+lgy=2a+b=2
当a=0,b=1时,lg(x2y)=2lgx+lgy=2a+b=1
故lg(x2y)的最大值为2
故答案为:2
|
即
|
令a=lgx,b=lgy,
则
|
满足条件的可行域如下图所示:

当a=-1,b=0时,lg(x2y)=2lgx+lgy=2a+b=-2
当a=1,b=0时,lg(x2y)=2lgx+lgy=2a+b=2
当a=0,b=1时,lg(x2y)=2lgx+lgy=2a+b=1
故lg(x2y)的最大值为2
故答案为:2

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目