题目内容
3.已知tanα是方程5x2-7x-6=0的根,且α∈($\frac{π}{2}$,π),求(1)$\frac{sin(\frac{π}{2}-α)•cos(3π-α)•ta{n}^{2}(π+α)}{sin(α+2π)•sin(2π-α)•tan(π-α)}$的值;
(2)求sin$\frac{10}{3}$π-$\sqrt{2}$cos(-$\frac{19}{4}$π)+tan(-$\frac{22}{3}$π)cos$\frac{5}{3}$π的值.
分析 (1)由已知可解得tanα=-$\frac{3}{5}$或2(舍去),由诱导公式化简所求后即可得解.
(2)利用诱导公式及特殊角的三角函数值即可化简求值.
解答 解:∵tanα是方程5x2-7x-6=0的根,且α∈($\frac{π}{2}$,π),
∴可解得:tanα=-$\frac{3}{5}$或2(舍去),
(1)$\frac{sin(\frac{π}{2}-α)•cos(3π-α)•ta{n}^{2}(π+α)}{sin(α+2π)•sin(2π-α)•tan(π-α)}$=$\frac{cosα•(-cosα)•ta{n}^{2}α}{sinα•(-sinα)•(-tanα)}$=$\frac{1}{\frac{3}{5}}$=$\frac{3}{5}$.
(2)sin$\frac{10}{3}$π-$\sqrt{2}$cos(-$\frac{19}{4}$π)+tan(-$\frac{22}{3}$π)cos$\frac{5}{3}$π
=(-sin$\frac{π}{3}$)-$\sqrt{2}$cos$\frac{3π}{4}$+tan$\frac{π}{3}$cos$\frac{2π}{3}$
=-$\frac{\sqrt{3}}{2}$+$\sqrt{2}×\frac{\sqrt{2}}{2}$-$\frac{\sqrt{3}}{2}$
=1-$\sqrt{3}$
点评 本题主要考查了运用诱导公式化简求值,同角三角函数基本关系的运用,一元二次方程的解法,属于基本知识的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.执行如图所示的程序框图,若输入的N是6,则输出P的值是( )
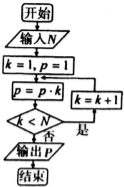

| A. | 120 | B. | 720 | C. | 1440 | D. | 5040 |