题目内容
12.设数列{an}的前n项和为Sn=$\frac{4}{3}$an-2n+1,n=1,2,3….(1)令bn=an+3•2n-1,求证:{bn}为等比数列,并求出{an};
(2)设cn=$\frac{{2}^{n}}{{S}_{n}+47}$,n=1,2,3…,求cn的最大值.
分析 (1)利用an=Sn-Sn-1可知当n≥2时$\frac{{b}_{n}}{{b}_{n-1}}$=4,进而计算即得结论;
(2)通过an=6•4n-1-3•2n-1,计算可知Sn=2•4n-3•2n+1,进而cn=$\frac{1}{2•{2}^{n}+\frac{48}{{2}^{n}}-3}$,利用基本不等式同时计算c2、c3并比较大小即可.
解答 (1)证明:∵Sn=$\frac{4}{3}$an-2n+1,
∴当n≥2时,an=Sn-Sn-1
=($\frac{4}{3}$an-2n+1)-($\frac{4}{3}$an-1-2n-1+1)
=$\frac{4}{3}$an-$\frac{4}{3}$an-1-2n-1,
∴an+3•2n-1=4(an-1+3•2n-2),即$\frac{{b}_{n}}{{b}_{n-1}}$=4,
又∵a1=S1=$\frac{4}{3}$a1-2+1,
∴a1=3,∴b1=a1+3•21-1=3+3=6,
∴数列{bn}是以6为首项、4为公比的等比数列,
∴bn=6•4n-1,
∴an=bn-3•2n-1=6•4n-1-3•2n-1;
(2)解:∵an=6•4n-1-3•2n-1,
∴Sn=$\frac{4}{3}$an-2n+1=$\frac{4}{3}$(6•4n-1-3•2n-1)-2n+1
=8•4n-1-4•2n-1-2n+1
=2•4n-2•2n-2n+1
=2•4n-3•2n+1,
∴cn=$\frac{{2}^{n}}{{S}_{n}+47}$=$\frac{{2}^{n}}{2•{4}^{n}-3•{2}^{n}+1+47}$=$\frac{1}{2•{2}^{n}+\frac{48}{{2}^{n}}-3}$,
∵2•2n+$\frac{48}{{2}^{n}}$≥2$\sqrt{2•{2}^{n}•\frac{48}{{2}^{n}}}$=8$\sqrt{6}$,当且仅当2•2n=$\frac{48}{{2}^{n}}$即n=$\frac{3+lo{g}_{2}3}{2}$时取等号,
∵1=log22<log23<log28=3,
∴2<n<3,
∵c2=$\frac{{2}^{2}}{2•{4}^{2}-3•{2}^{2}+48}$=$\frac{1}{17}$,
c3=$\frac{{2}^{3}}{2•{4}^{3}-3•{2}^{3}+48}$=$\frac{1}{19}$,
∴cn的最大值为$\frac{1}{17}$.
点评 本题考查等比数列的判定及通项,考查运算求解能力,注意解题方法的积累,属于中档题.

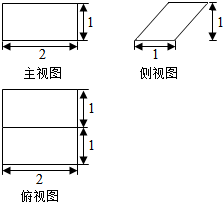
| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | $\frac{2}{3}$ |
| A. | ($\frac{3}{4}$,$\frac{9}{10}$) | B. | ($\frac{1}{2}$,$\frac{9}{10}$) | C. | ($\frac{3}{5}$,$\frac{3}{4}$) | D. | ($\frac{1}{2}$,$\frac{3}{4}$) |
| A. | $\frac{12-8ln2}{1-2ln2}$ | B. | $\frac{2}{1-2ln2}$ | C. | $\frac{4}{1-2ln2}$ | D. | -2 |