题目内容
11.$\underset{lim}{n→∞}$$\frac{1}{n}$($\frac{1}{n}$+$\frac{2}{n}$+…+$\frac{n-1}{n}$+1)写成定积分是${∫}_{0}^{1}$f(x)dx.分析 根据定积分的概念和写法填空即可.
解答 解:$\underset{lim}{n→∞}$$\frac{1}{n}$($\frac{1}{n}$+$\frac{2}{n}$+…+$\frac{n-1}{n}$+1)写成定积分是${∫}_{0}^{1}$f(x)dx.
故答案是:${∫}_{0}^{1}$f(x)dx.
点评 本题考查了定积分的背景.定积分${∫}_{0}^{1}$f(x)dx是一个常数,即Sn无限趋近的常数S(n→+∞时)记为${∫}_{0}^{1}$f(x)dx,而不是Sn.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
20.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | $\frac{2}{3}$ |
20.在△ABC中,角A为钝角,AB=1,AC=3,AD为BC边上的高,已知$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x的取值范围为( )
| A. | ($\frac{3}{4}$,$\frac{9}{10}$) | B. | ($\frac{1}{2}$,$\frac{9}{10}$) | C. | ($\frac{3}{5}$,$\frac{3}{4}$) | D. | ($\frac{1}{2}$,$\frac{3}{4}$) |
1.已知f′(x)是函数f(x)的导数,f(x)=f′(1)•2x+x2,f′(2)=( )
| A. | $\frac{12-8ln2}{1-2ln2}$ | B. | $\frac{2}{1-2ln2}$ | C. | $\frac{4}{1-2ln2}$ | D. | -2 |
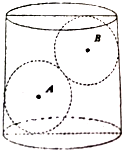 如图,在水平放置的直径与高相等的圆柱内,放入两个半径相等的小球(球A和球B),圆柱的底面直径为2+$\sqrt{2}$,向圆柱内注满水,水面刚好淹没小球B
如图,在水平放置的直径与高相等的圆柱内,放入两个半径相等的小球(球A和球B),圆柱的底面直径为2+$\sqrt{2}$,向圆柱内注满水,水面刚好淹没小球B