题目内容
12．执行如图所示的程序框图，若输入的N是6，则输出P的值是（ ）
| A． | 120 | B． | 720 | C． | 1440 | D． | 5040 |
分析 根据程序框图进行模拟计算即可．
解答 解：P=1×1=1，1＜N成立，循环K=2，
P=1×2=2，2＜N成立，循环K=3，
P=2×3=6，3＜N成立，循环K=4，
P=6×4=24，4＜N成立，循环K=5，
P=24×5=120，5＜N成立，循环K=6，
P=120×6=720，6＜N不成立，
输出P=720，
故选：B
点评 本题主要考查程序框图的应用，根据条件进行模拟计算是解决本题的关键．
练习册系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
2．化简（x+1）4-4（x+1）3+6（x+1）2-4（x+1）+1的结果为（ ）
| A． | x4 | B． | （x-1）4 | C． | （x+1）4 | D． | x4-1 |
3．设a=0.82.1，b=21.1，c=log23，则（ ）
| A． | b＜c＜a | B． | c＜a＜b | C． | a＜b＜c | D． | a＜c＜b |
20．某几何体的三视图如图所示，则该几何体的体积为（ ）
| A． | 1 | B． | 2 | C． | 2$\sqrt{2}$ | D． | $\frac{2}{3}$ |
7．
一次考试中，五名学生的数学、物理成绩如下表所示：
（1）要在这五名学生中选2名参加一项活动，求选中的同学中至少有一人的物理成绩高于90分的概率．
（2）根据上表数据，用变量y与x的相关系数和散点图说明物理成绩y与数学成绩x之间线性相关关系的强弱，如果具有较强的线性相关关系，求y与x的线性回归方程（系数精确到0.01）；如果不具有线性相关关系，请说明理由．
参考公式：
相关系数r=$\frac{\sum_{i=1}^{n}{（x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sqrt{\sum_{i=1}^{n}（{x}_{i-}\overline{x}）^2\sum_{i=1}^{n}（{y}_{i}-\overline{y}）^2}}$
回归直线的方程：$\widehat{y}$=$\widehat{b}x+\widehat{a}$，其中$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^2}$，$\widehat{a}=\widehat{y}-\widehat{b}x$，$\widehat{{y}_{i}}$是与xi对应的回归估计值．
参考数据：$\overline{x}$=93，$\overline{y}$=90，$\sum_{i=1}^{n}{（x}_{i}-\overline{x}）^2$=40，$\sum_{i=1}^{n}（{y}_{i}-\overline{y}）^2$=24，$\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）$=30，$\sqrt{40}$≈6.32，$\sqrt{24}$≈4.90．
一次考试中，五名学生的数学、物理成绩如下表所示：| 学生 | A1 | A2 | A3 | A4 | A5 |
| 数学 | 89 | 91 | 93 | 95 | 97 |
| 物理 | 87 | 89 | 89 | 92 | 93 |
（2）根据上表数据，用变量y与x的相关系数和散点图说明物理成绩y与数学成绩x之间线性相关关系的强弱，如果具有较强的线性相关关系，求y与x的线性回归方程（系数精确到0.01）；如果不具有线性相关关系，请说明理由．
参考公式：
相关系数r=$\frac{\sum_{i=1}^{n}{（x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sqrt{\sum_{i=1}^{n}（{x}_{i-}\overline{x}）^2\sum_{i=1}^{n}（{y}_{i}-\overline{y}）^2}}$
回归直线的方程：$\widehat{y}$=$\widehat{b}x+\widehat{a}$，其中$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^2}$，$\widehat{a}=\widehat{y}-\widehat{b}x$，$\widehat{{y}_{i}}$是与xi对应的回归估计值．
参考数据：$\overline{x}$=93，$\overline{y}$=90，$\sum_{i=1}^{n}{（x}_{i}-\overline{x}）^2$=40，$\sum_{i=1}^{n}（{y}_{i}-\overline{y}）^2$=24，$\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）$=30，$\sqrt{40}$≈6.32，$\sqrt{24}$≈4.90．
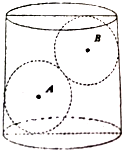如图，在水平放置的直径与高相等的圆柱内，放入两个半径相等的小球（球A和球B），圆柱的底面直径为2+$\sqrt{2}$，向圆柱内注满水，水面刚好淹没小球B