题目内容
8.求平行于直线2x+y-1=0且与圆(x-2)2+y2=4相切的直线方程.分析 设出所求直线方程,利用圆心到直线的距离等于半径,求出直线方程中的变量,即可求出直线方程.
解答 解:设所求直线方程为2x+y+b=0,
因为平行于直线2x+y-1=0且与圆(x-2)2+y2=4相切,
所以$\frac{|4+b|}{\sqrt{{2}^{2}+1}}$=2,所以b=-4±2$\sqrt{5}$,
所以所求直线方程为:2x+y-4+2$\sqrt{5}$=0或2x+y-4-2$\sqrt{5}$=0.
点评 本题考查两条直线平行的判定,圆的切线方程,考查计算能力,是基础题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
16.某几何体的三视图如图,则该几何体的体积为( )
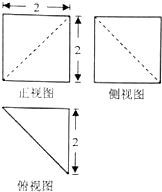

| A. | $\frac{8}{3}$ | B. | $\frac{8\sqrt{2}}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
20.在△ABC中,角A为钝角,AB=1,AC=3,AD为BC边上的高,已知$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x的取值范围为( )
| A. | ($\frac{3}{4}$,$\frac{9}{10}$) | B. | ($\frac{1}{2}$,$\frac{9}{10}$) | C. | ($\frac{3}{5}$,$\frac{3}{4}$) | D. | ($\frac{1}{2}$,$\frac{3}{4}$) |
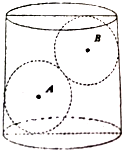 如图,在水平放置的直径与高相等的圆柱内,放入两个半径相等的小球(球A和球B),圆柱的底面直径为2+$\sqrt{2}$,向圆柱内注满水,水面刚好淹没小球B
如图,在水平放置的直径与高相等的圆柱内,放入两个半径相等的小球(球A和球B),圆柱的底面直径为2+$\sqrt{2}$,向圆柱内注满水,水面刚好淹没小球B