题目内容
11.已知函数f(x)=lnx(x>0).(1)求g(x)=xf(x),求函数y=g(x)的极值;
(2)判断函数h(x)=x2f(x)+x的单调性,并证明;
(3)若对任意两个互不相等的正数x1,x2,都有$\frac{{{f(x}_{1})-f(x}_{2})}{{x}_{1}-{x}_{2}}$<kf′($\sqrt{{x}_{1}{x}_{2}}$)恒成立,求实数k的最小值.
分析 (1)先求出函数g(x)的导数,得到函数的单调区间,从而求出函数g(x)的极值;
(2)根据g(x)的范围求出函数h(x)的导数,从而得到函数的单调性;
(3)所证问题转化为ln$\frac{{x}_{2}}{{x}_{1}}$<k($\sqrt{\frac{{x}_{2}}{{x}_{1}}}$-$\sqrt{\frac{{x}_{1}}{{x}_{2}}}$),(*)令$\sqrt{\frac{{x}_{2}}{{x}_{1}}}$=t,则(*)?2lnt<k(t-$\frac{1}{t}$),(t>1),设φ(t)=k(t-$\frac{1}{t}$)>-2lnt,则原命题等价于φ(t)=k(t-$\frac{1}{t}$)-2lnt>0在(1,+∞)上恒成立,通过讨论k的范围,得到函数φ(x)的单调性,从而求出k的最小值.
解答 解:(1)g(x)=xlnx,g′(x)=lnx+1,
由g′(x)=0得x=$\frac{1}{e}$,
| x | (0,$\frac{1}{e}$) | $\frac{1}{e}$ | ($\frac{1}{e}$,+∞) |
| g′(x) | - | 0 | + |
| g(x) | 递减 | -$\frac{1}{e}$ | 递增 |
(2)函数h(x)在(0,+∞)单调递增,
h(x)=x2lnx+x,h′(x)=2xlnx+x+1,
由(1)得:g(x)=xlnx≥-$\frac{1}{e}$,且x>0,
∴h′(x)=2xlnx+x+1>0,
∴函数h(x)在(0,+∞)单调递增;
(3)不妨设x1<x2,f′(x)=$\frac{1}{x}$,
$\frac{f{(x}_{1})-f{(x}_{2})}{{x}_{1}{-x}_{2}}$<kf′($\sqrt{{x}_{1}{•x}_{2}}$)
?$\frac{l{nx}_{2}-l{nx}_{1}}{{x}_{2}{-x}_{1}}$<$\frac{k}{\sqrt{{{x}_{1}x}_{2}}}$
?ln$\frac{{x}_{2}}{{x}_{1}}$<k•$\frac{{x}_{2}{-x}_{1}}{\sqrt{{{x}_{1}x}_{2}}}$=k($\sqrt{\frac{{x}_{2}}{{x}_{1}}}$-$\sqrt{\frac{{x}_{1}}{{x}_{2}}}$),(*),
令$\sqrt{\frac{{x}_{2}}{{x}_{1}}}$=t,则(*)?2lnt<k(t-$\frac{1}{t}$),(t>1),
设φ(t)=k(t-$\frac{1}{t}$)>-2lnt,
则原命题等价于φ(t)=k(t-$\frac{1}{t}$)-2lnt>0在(1,+∞)上恒成立,
φ′(t)=$\frac{{kt}^{2}-2t+k}{{t}^{2}}$,
①当k≤0时,φ′(t)≤0,φ(t)在(1,+∞)上单调递减,φ(t)<φ(1)=0,
故k≤0不符合题意;
②当k>0时,
(i)当△=4-4k2≤0,即k≥1时,φ′(t)≥0,φ(t)在(1,+∞)单调递增,
φ(t)>φ(1)=0,故k≥1符号题意;
(ii)当0<k<1时,△=4-4k2>0,
设方程kt2-2t+k=0的两根分别是t1,t2,且t1<t2,
则0<t1<1<t2且当t∈(1,t2]时,φ′(t)≤0,当t∈[t2,+∞)时,φ′(t)≥0,
∴φ(t)在[1,t2)上单调递减,在(t2,+∞)上单调递增,
故φ(t2)<φ(1)=0与φ(t)>0在(1,+∞)是恒成立矛盾,
故0<k<1不符号题意,
综上,实数k的最小值为1.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,函数恒成立问题,考查换元思想、分类讨论思想,第(3)问较复杂,解题时仔细谨慎,本题属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.化简(x+1)4-4(x+1)3+6(x+1)2-4(x+1)+1的结果为( )
| A. | x4 | B. | (x-1)4 | C. | (x+1)4 | D. | x4-1 |
16.某几何体的三视图如图,则该几何体的体积为( )
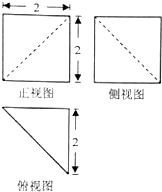

| A. | $\frac{8}{3}$ | B. | $\frac{8\sqrt{2}}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
3.设a=0.82.1,b=21.1,c=log23,则( )
| A. | b<c<a | B. | c<a<b | C. | a<b<c | D. | a<c<b |
20.某几何体的三视图如图所示,则该几何体的体积为( )
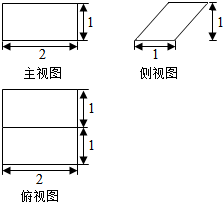

| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | $\frac{2}{3}$ |