题目内容
已知数列{ }满足
}满足 ,且
,且
(1)求证:数列{ }是等差数列;
}是等差数列;
(2)求数列{ }的通项公式;
}的通项公式;
(3)设数列{ }的前
}的前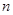 项之和
项之和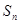 ,求证:
,求证: .
.
(1)利用等差数列的定义证明;(2) ;(3)先求和然后再利用放缩法证明
;(3)先求和然后再利用放缩法证明
解析试题分析:(1)
 ,即
,即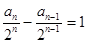

 数列
数列 是等差数列,公差为
是等差数列,公差为 ,首项
,首项
(2)由(1)得 ,
,
(3)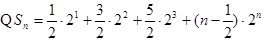 (1)
(1) (2)
(2)


考点:本题考查了数列的通项公式及前N项和
点评:数列的通项公式及应用是数列的重点内容,数列的大题对逻辑推理能力有较高的要求,在数列中突出考查学生的理性思维,这是近几年新课标高考对数列考查的一个亮点,也是一种趋势.随着新课标实施的深入,高考关注的重点为等差、等比数列的通项公式,错位相减法、裂项相消法等求数列的前n项的和等等

练习册系列答案
相关题目
 的前
的前 项和
项和 (
( ,求证:数列
,求证:数列 是等差数列,并求数列
是等差数列,并求数列 ,
, ,求使得
,求使得 成立的最小正整数
成立的最小正整数 ,
, 、
、 、
、 是平面直角坐标系上的三点,且
是平面直角坐标系上的三点,且 、
、 、
、 成等差数列,公差为
成等差数列,公差为 ,
, .
. ,
,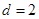 ,点
,点 上时,求点
上时,求点 的方程是
的方程是
 ,过点
,过点 的直线交圆于
的直线交圆于 两点,
两点, 是圆
是圆 上,点
上,点 ,求证:线段
,求证:线段 的垂直平分线与
的垂直平分线与 轴的交点为一定点,并求该定点的坐标.
轴的交点为一定点,并求该定点的坐标. 的前三项和为18,
的前三项和为18, 是一个与
是一个与 无关的常数,若
无关的常数,若 恰为等比数列
恰为等比数列 的前三项,(1)求
的前三项,(1)求 ,
, 的前三
的前三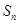 ,求证:
,求证:
 满足
满足 ,
, ;数列
;数列 满足
满足 ,
,  .
. 和
和 的通项公式;
的通项公式; 、
、 的前
的前 项和
项和 ,
, .
. 满足
满足
 。
。 ,
,  为
为 项和,求
项和,求 。
。 中,
中, ,不等式
,不等式
 对任意
对任意 都成立.
都成立. 的取值范围;
的取值范围; ,
, ,求证:对任意的
,求证:对任意的 .
. 是一个等差数列,且
是一个等差数列,且 ,
, .
. ; (Ⅱ)求
; (Ⅱ)求 的前
的前 项和为
项和为 ,已知
,已知 ,
, (
(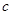 为常数,
为常数, ),且
),且 成等差数列.
成等差数列. 是首项为1,公比为
是首项为1,公比为


 ,(
,(