题目内容
已知点 ,
, 、
、 、
、 是平面直角坐标系上的三点,且
是平面直角坐标系上的三点,且 、
、 、
、 成等差数列,公差为
成等差数列,公差为 ,
, .
.
(1)若 坐标为
坐标为 ,
,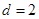 ,点
,点 在直线
在直线 上时,求点
上时,求点 的坐标;
的坐标;
(2)已知圆 的方程是
的方程是
 ,过点
,过点 的直线交圆于
的直线交圆于 两点,
两点, 是圆
是圆 上另外一点,求实数
上另外一点,求实数 的取值范围;
的取值范围;
(3)若 、
、 、
、 都在抛物线
都在抛物线 上,点
上,点 的横坐标为
的横坐标为 ,求证:线段
,求证:线段 的垂直平分线与
的垂直平分线与 轴的交点为一定点,并求该定点的坐标.
轴的交点为一定点,并求该定点的坐标.
(1)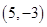 或
或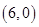 (2)当
(2)当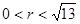 时,
时,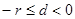 或
或 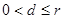 ;当
;当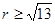 时,
时,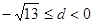 或
或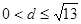
(3)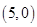
解析试题分析:解(1)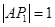 ,所以
,所以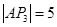 ,设
,设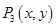
则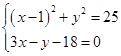 ,消去
,消去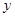 ,得
,得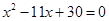 ,…(2分)
,…(2分)
解得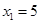 ,
,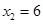 ,所以
,所以 的坐标为
的坐标为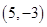 或
或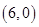
(2)由题意可知点 到圆心的距离为
到圆心的距离为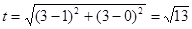 …(6分)
…(6分)
(ⅰ)当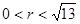 时,点
时,点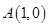 在圆上或圆外,
在圆上或圆外, ,
,
又已知 ,
,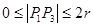 ,所以
,所以 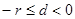 或
或 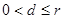
(ⅱ)当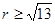 时,点
时,点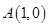 在圆内, 所以
在圆内, 所以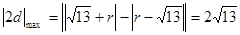 ,
,
又已知  ,
,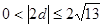 ,即
,即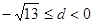 或
或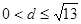
结论:当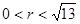 时,
时,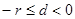 或
或 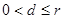 ;当
;当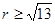 时,
时,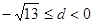 或
或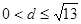
(3)因为抛物线方程为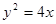 ,所以
,所以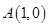 是它的焦点坐标,点
是它的焦点坐标,点 的横坐标为
的横坐标为 ,即
,即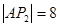
设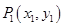 ,
,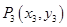 ,则
,则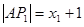 ,
,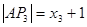 ,
,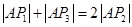 ,
,
所以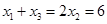
直线 的斜率
的斜率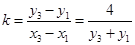 ,则线段
,则线段 的垂直平分线
的垂直平分线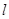 的斜率
的斜率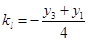
则线段 的垂直平分线
的垂直平分线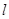 的方程为
的方程为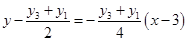
直线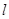 与
与 轴的交点为定点
轴的交点为定点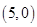
考点:直线与圆,抛物线
点评:解决的关键是利用直线与圆的位置关系,以及抛物线的几何性质来求解斜率和中垂线方程,属于中档题。

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
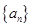 中,点
中,点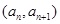
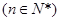 在直线
在直线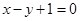 上,且
上,且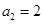 .
. 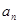 ;
;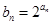 ,数列
,数列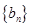 的前
的前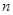 项和为
项和为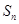 ,
,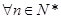 ,
,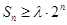 成立,求实数
成立,求实数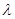 的取值范围.
的取值范围.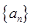 首项为1,且
首项为1,且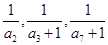 成等比数列,
成等比数列,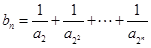
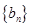 通项公式;
通项公式;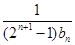 前n项和
前n项和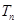 ;
;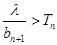 成立,求
成立,求 范围.
范围. 中,当
中,当 时,总有
时,总有 成立,且
成立,且 .
. 是等差数列,并求数列
是等差数列,并求数列 项和
项和 .
. 满足:
满足: ,
, .
. .
.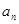 及
及 (n
(n N*),求数列
N*),求数列 的前n项和
的前n项和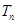 .
. 满足
满足 ,
, 。
。 项和
项和 及使得
及使得 是等差数列,且
是等差数列,且
 项的和
项的和
 ,求
,求 的前
的前
 }满足
}满足 ,且
,且
 }是等差数列;
}是等差数列;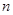 项之和
项之和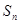 ,求证:
,求证: .
. }的前n项和为
}的前n项和为 ,已知
,已知 ,
, .
.
 ,求数列{
,求数列{ }的前项和
}的前项和 .
.