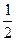题目内容
已知数列{an}的通项为an=26-2n，．若要使此数列的前n项和最大，则n的值为（ ）
| A．12 | B．13 | C．12或13 | D．14 |
∵an=26-2n，
∴an+1-an=（24-2n）-（26-2n）=-2，
∴数列{an}是公差为-2的等差数列，首项a1=24，
令an=26-2n≤0，可得n≥13
∴数列{an}的前12项为正数，第13项为0，从第14项开始为负数，
∴数列的前12项，或前13项和最大，
故选：C
∴an+1-an=（24-2n）-（26-2n）=-2，
∴数列{an}是公差为-2的等差数列，首项a1=24，
令an=26-2n≤0，可得n≥13
∴数列{an}的前12项为正数，第13项为0，从第14项开始为负数，
∴数列的前12项，或前13项和最大，
故选：C
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
, 则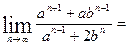
（ ）
