题目内容
已知数列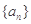 的前n项和为构成数列
的前n项和为构成数列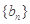 ,数列
,数列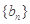 的前n项和构成数列
的前n项和构成数列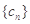 .
.
若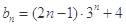 ,则
,则
(1)求数列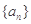 的通项公式;
的通项公式;
(2)求数列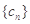 的通项公式.
的通项公式.
(1) ;(2)
;(2)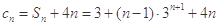
解析试题分析:(1)数列的项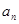 与前
与前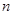 项和
项和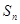 的关系是:
的关系是: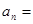
 ,检验
,检验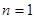 时是否满足上式,如果满足合写成一个,如果不满足,分段来写,此题已知数列
时是否满足上式,如果满足合写成一个,如果不满足,分段来写,此题已知数列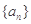 的前
的前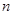 项和,所以可直接求通项公式;
项和,所以可直接求通项公式;
(2)求数列前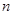 项和时,首先观察通项公式的形式,选择合适的求和方法,常见的求和方法有:①裂项相消法(把通项公式裂成两项的差,在求和过程相互抵消);②错位相减法(通项公式是等差乘以等比的形式);③分组求和法(一般就是根据加法结合律,把求和问题转化为等差求和以及等比求和);④奇偶并项求和法(一般像这种
项和时,首先观察通项公式的形式,选择合适的求和方法,常见的求和方法有:①裂项相消法(把通项公式裂成两项的差,在求和过程相互抵消);②错位相减法(通项公式是等差乘以等比的形式);③分组求和法(一般就是根据加法结合律,把求和问题转化为等差求和以及等比求和);④奇偶并项求和法(一般像这种 乘以等差数列,可以分析相邻项的特点),观察
乘以等差数列,可以分析相邻项的特点),观察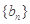 的通项公式,可利用错位相减法和分组求和法求解.
的通项公式,可利用错位相减法和分组求和法求解.
试题解析:(1)当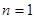 时,
时,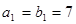 2分
2分
当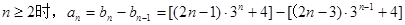 4分
4分
=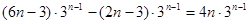
综上所述: 6分
6分
(2)
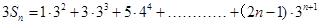 7分
7分
相减得: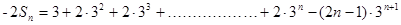
=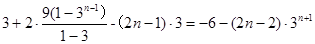 10分
10分
所以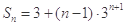 12分
12分
因此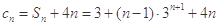 14分
14分
考点:1、前n项和与通项公式的关系;2、数列求和.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 )+f(
)+f( )+f(
)+f(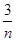 )+…+f(
)+…+f(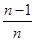 )+f(1).
)+f(1).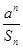 (a∈R)且bn<bn+1对所有正整数n恒成立,求a的取值范围.
(a∈R)且bn<bn+1对所有正整数n恒成立,求a的取值范围.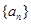 的前项和为
的前项和为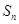 ,且满足
,且满足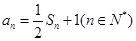 ;
;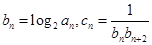 ,且
,且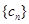 的前n项和为
的前n项和为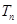 ,求使得
,求使得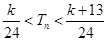 对
对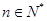 都成立的所有正整数k的值.
都成立的所有正整数k的值. 中,
中,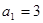 ,其前
,其前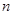 项和为
项和为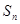 ,等比数列
,等比数列 的各项均为正数,
的各项均为正数,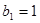 ,公比为
,公比为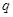 ,且
,且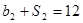 ,
, .
.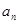 与
与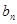 ;
;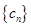 满足
满足 ,求
,求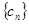 的前
的前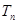 .
.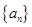 中,
中,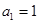 ,前
,前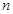 项的和是
项的和是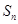 ,且
,且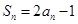 ,
,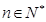 .
.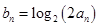 ,求
,求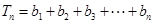 .
. 的公差
的公差 大于0,且
大于0,且 是方程
是方程 的两根,数列
的两根,数列 的前
的前 项和为
项和为 .
. 的通项公式;
的通项公式; ,求证:
,求证: ;
; 的前
的前 .
.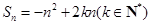 ,且
,且 的最大值为4.
的最大值为4.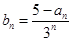 ,数列{bn}的前n项和为Tn,试比较Tn与
,数列{bn}的前n项和为Tn,试比较Tn与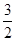 的大小.
的大小. 中,
中, ,
,
 且
且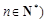 .
. ,
,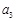 的值;
的值; 是等比数列,并求
是等比数列,并求 项和
项和 .
.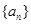 的首项
的首项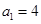 ,且
,且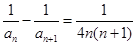 (
( N*),数列
N*),数列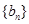 的前
的前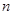 项和
项和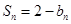 。
。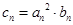 ,证明:当且仅当
,证明:当且仅当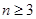 时,
时, 。
。