题目内容
在数列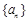 中,
中, ,
,
 且
且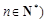 .
.
(1)求 ,
,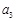 的值;
的值;
(2)证明:数列 是等比数列,并求
是等比数列,并求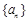 的通项公式;
的通项公式;
(3)求数列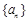 的前
的前 项和
项和 .
.
(1)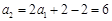 ,
,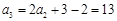 .
.
(2)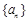 的通项公式为
的通项公式为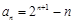
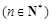 .
.
(3)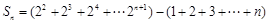
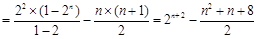
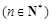 .
.
解析试题分析:(1)解:∵ ,
,
 且
且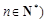 ,
,
∴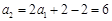 ,
,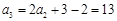 . 2分
. 2分
(2)证明:
∵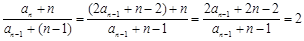 ,
,
∴数列 是首项为
是首项为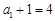 ,公比为
,公比为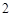 的等比数列.
的等比数列.
∴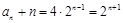 ,即
,即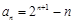 ,
,
∴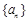 的通项公式为
的通项公式为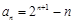
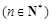 . 8分
. 8分
(3)∵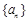 的通项公式为
的通项公式为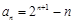
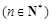 ,
,
∴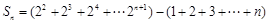
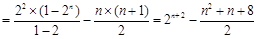
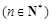 . 12分
. 12分
考点:数列的递推公式,数列的通项公式,等差数列、等比数列的证明,“分组求和法”。
点评:中档题,首先根据递推公式,确定得到 的表达式。进一步确定数列的通项公式
的表达式。进一步确定数列的通项公式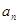 。 “分组求和法”“裂项相消法”“错位相减法”是高考常常考查的数列求和方法。
。 “分组求和法”“裂项相消法”“错位相减法”是高考常常考查的数列求和方法。

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
 的相邻两项
的相邻两项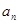 ,
,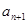 是关于
是关于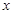 方程
方程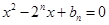 的两根,且
的两根,且 .
.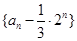 是等比数列;
是等比数列;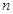 项和
项和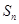 ;
;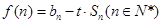 ,若
,若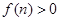 对任意的
对任意的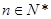 都成立,求实数
都成立,求实数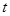 的取值范围.
的取值范围.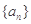 的前n项和为构成数列
的前n项和为构成数列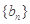 ,数列
,数列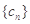 .
.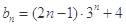 ,则
,则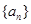 的前
的前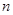 项和
项和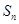 满足
满足 ,
,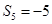 。
。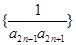 的前
的前 满足:
满足: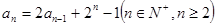 且
且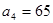 .(1)求数列
.(1)求数列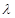 ,使数列
,使数列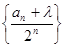 为等差数列?若存在,求出
为等差数列?若存在,求出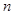 项和
项和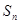 .
. ,数列
,数列 的前n项和
的前n项和 ,且
,且 同时满足:
同时满足: ,使得不等式
,使得不等式 成立.
成立. 的图像上一点,数列
的图像上一点,数列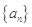 的前n项和
的前n项和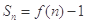 .
. 的前
的前 项和为
项和为 ,
,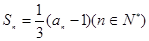
 ;
; 的各项均为正数,
的各项均为正数, 为其前
为其前 项和,且对任意的
项和,且对任意的 ,有
,有 .
. ,求数列
,求数列 的前
的前 .
.