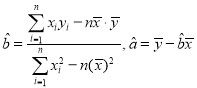题目内容
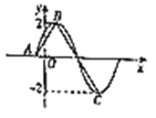
【题目】已知函数
的部分图像如图所示，若
，
，
分别为最高点与最低点，
为图象与
轴交点，且
的面积为
.
（1）求函数
的单调递增区间；
（2）若将的图像向左平移
个单位长度，得到函数
的图像，求函数在区间
上的最大值和最小值.
【答案】(1) 
，
. (2) 最大值
，最小值-2.
【解析】
（1）根据图像求得
，令
，，解不等式，即可得到函数
的单调递增区间；
（2）根据函数图像平移法则可得
，再根据
，利用正弦函数的定义域和值域求得函数
的最值。
（1）由
可得
，即
.
又因为
，所以
.
由题意
的面积为
，所以
.故
，
所以，
由，，解得
，，
所以函数的单调递增区间为，.
（2）由题意将的图像向左平移
个单位长度，得到函数
的图像，
∴
.
∵，∴
.
∴当
时，
，取得最大值，
当
时，
，取得最小值-2.
练习册系列答案
相关题目
【题目】假设某种设备使用的年限
（年）与所支出的维修费用
（万元）有以下统计资料：
使用年限 | 2 | 3 | 4 | 5 | 6 |
维修费用 | 2 | 4 | 5 | 6 | 7 |
若由资料知对呈线性相关关系.试求：
（1）求
；
（2）线性回归方程
；
（3）估计使用10年时，维修费用是多少？
附：利用“最小二乘法”计算
的值时，可根据以下公式：
