题目内容
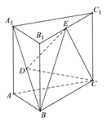
【题目】如图，直三棱柱ABC﹣A1B1C1中，AC=BC= 
AA1 ， D是棱AA1的中点，DC1⊥BD 
（1）证明：DC1⊥BC；
（2）求二面角A1﹣BD﹣C1的大小．
【答案】
（1）证明：在Rt△DAC中，AD=AC，∴∠ADC=45°
同理：∠A1DC1=45°，∴∠CDC1=90°
∴DC1⊥DC，DC1⊥BD
∵DC∩BD=D
∴DC1⊥面BCD
∵BC面BCD
∴DC1⊥BC
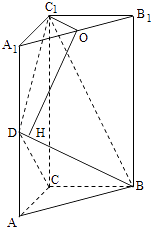
（2）解：∵DC1⊥BC，CC1⊥BC，DC1∩CC1=C1，∴BC⊥面ACC1A1，
∵AC面ACC1A1，∴BC⊥AC
取A1B1的中点O，过点O作OH⊥BD于点H，连接C1O，OH
∵A1C1=B1C1，∴C1O⊥A1B1，
∵面A1B1C1⊥面A1BD，面A1B1C1∩面A1BD=A1B1，
∴C1O⊥面A1BD
而BD面A1BD
∴BD⊥C1O，
∵OH⊥BD，C1O∩OH=O，
∴BD⊥面C1OH∴C1H⊥BD，∴点H与点D重合且∠C1DO是二面角A1﹣BD﹣C1的平面角
设AC=a，则 
， 
，
∴sin∠C1DO= 
∴∠C1DO=30°
即二面角A1﹣BD﹣C1的大小为30°
【解析】（1）证明DC1⊥BC，只需证明DC1⊥面BCD，即证明DC1⊥DC，DC1⊥BD；（2）证明BC⊥面ACC1A1 ， 可得BC⊥AC取A1B1的中点O，过点O作OH⊥BD于点H，连接C1O，C1H，可得点H与点D重合且∠C1DO是二面角A1﹣BD﹣C1的平面角，由此可求二面角A1﹣BD﹣C1的大小．
【考点精析】掌握空间中直线与直线之间的位置关系是解答本题的根本，需要知道相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点．
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
