题目内容
【题目】如图,已知圆O的内接四边形BCED,BC为圆O的直径,BC=2,延长CB,ED交于A点,使得∠DOB=∠ECA,过A作圆O的切线,切点为P,
(1)求证:BD=DE;
(2)若∠ECA=45°,求AP2的值.
【答案】
(1)证明:连结OE,∵圆O的内接四边形BCED,BC为圆O的直径,
BC=2,延长CB,ED交于A点,使得∠DOB=∠ECA,
∴CE∥OD,∴∠CEO=∠EOD,
∵CO=EO,∴∠OCE=∠OEC,
∴∠BOD=∠EOD,
∴BD=DE.
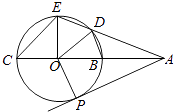
(2)解:解:(2)∵∠ECA=45°,BC为圆O的直径,BC=2,
∴∠COE=90°,∴CE= ![]() ,OD=1,
,OD=1,
∵OD∥CE,∴ ![]() =
= ![]() ,解得AB=
,解得AB= ![]() ,
,
∵过A作圆O的切线,切点为P,
∴AP2=AB(AB+2)= ![]() =2+2
=2+2 ![]()
【解析】(1)连结OE,由已知得CE∥OD,从而∠BOD=∠EOD,由此能证明BD=DE.(2)推导出∠COE=90°,CE= ![]() ,OD=1,AB=
,OD=1,AB= ![]() ,由此利用切割线定理能求出AP2 .
,由此利用切割线定理能求出AP2 .

练习册系列答案
相关题目
【题目】石嘴山三中最强大脑社对高中学生的记忆力x和判断力y进行统计分析,得下表数据
x | 6 | 8 | 10 | 12 |
y | 2 | 3 | 5 | 6 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ,预测记忆力为9的同学的判断力.
,预测记忆力为9的同学的判断力.
(2)若记忆力增加5个单位,预测判断力增加多少个单位?
参考公式: