题目内容
若tanα=lg(10a),tanβ=lg(
),且α+β=
,则实数a的值为( )
| 1 |
| a |
| π |
| 4 |
| A、1 | ||
B、
| ||
C、1或
| ||
| D、1或10 |
考点:两角和与差的正切函数,对数的运算性质
专题:计算题,三角函数的求值
分析:由已知可得1=
,由对数的运算性质即可解得实数a的值.
lg(10a)+lg(
| ||
1-lg(10a)lg(
|
解答:
解:∵tanα=lg(10a),tanβ=lg(
),且α+β=
,
∴tan(α+β)=tan
=1=
=
,
∴lg(10a)+lg(
)=lg10=1=1-lg(10a)lg(
)
∴lg(10a)lg(
)=0
∴10a=1,或
=1
∴a=
或1.
故选:C.
| 1 |
| a |
| π |
| 4 |
∴tan(α+β)=tan
| π |
| 4 |
| tanα+tanβ |
| 1-tanαtanβ |
lg(10a)+lg(
| ||
1-lg(10a)lg(
|
∴lg(10a)+lg(
| 1 |
| a |
| 1 |
| a |
∴lg(10a)lg(
| 1 |
| a |
∴10a=1,或
| 1 |
| a |
∴a=
| 1 |
| 10 |
故选:C.
点评:本题主要考察了两角和与差的正切函数,对数的运算性质,属于基本知识的考查.

练习册系列答案
相关题目
命题“?x0∈R,x>1”否定是( )
| A、?x∈R,x>1 |
| B、?x0∈R,x0≤1 |
| C、?x∈R,x≤1 |
| D、?x0∈R,x0<1 |
在△ABC中,下列等式恒成立的是( )
| A、csinA=asinB |
| B、bcosA=acosB |
| C、asinA=bsinB |
| D、asinB=bsinA |
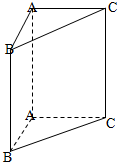 如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=
如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=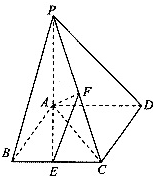 如图,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥面ABCD,AP=AB,E、F分别是BC、PC的中点.
如图,四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠ABC=60°,PA⊥面ABCD,AP=AB,E、F分别是BC、PC的中点.