Question

【题目】某老师对全班名学生学习积极性和参加社团活动情况进行调查，统计数据如下所示：

	参加社团活动	不参加社团活动	合计
学习积极性高
学习积极性一般
合计

（1）请把表格数据补充完整；

（2）若从不参加社团活动的人按照分层抽样的方法选取人，再从所选出的人中随机选取两人作为代表发言，求至少有一个学习积极性高的概率；

（3）运用独立性检验的思想方法分析：请你判断是否有的把握认为学生的学习积极性与参与社团活动由关系？

附：

Answer 1

【答案】（1）见解析；（2）；（3）有的把握认为学生的学习积极性与参与社团活动由关系.

【解析】试题分析：（1）根据列联表给出的数据可以补全其它数据（2）人选人，其中学习积极性高的人记为，学习积极性一般的人，记为，从这人中任选两人，共有以下个等可能性基本事件： ，

则至少有以为学习积极性高的事件有个，根据古典概型的概率计算即得解.

（3）根据列联表中所给的数据，代入求这组数据的观测值的公式，求出观测值，把观测值同临界值进行比较，得到有99.9%的把握认为学生的学习积极性与参加社团活动情况有关系．

试题解析：

（1）

	参加社团活动	不参加社团活动	合计
学习积极性高
学习积极性一般
合计

（2）人选人，其中学习积极性高的人记为，学习积极性一般的人，记为，从这人中任选两人，共有以下个等可能性基本事件： ，

则至少有以为学习积极性高的事件有个，所以至少有一位学习积极性高的概率.

（3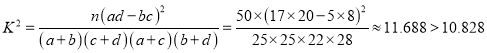）所以大约有的把握认为学生的学习积极性与参与社团活动由关系.