题目内容
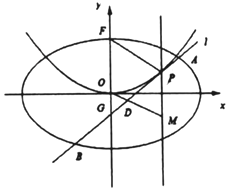
【题目】已知定义在正实数集上的函数![]() ,其中
,其中![]() ,设两曲线
,设两曲线![]() 有公共点,且在公共点处的切线相同.
有公共点,且在公共点处的切线相同.
(1)若![]() ,求实数
,求实数![]() 的值;
的值;
(2)用![]() 表示
表示![]() ,并求实数
,并求实数![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)设y=f(x)与y=g(x)(x>0)在公共点(x0,y0)处的切线相同,先利用导数求出在切点处的导函数值,再结合导数的几何意义即可求出切线的斜率.最后利用两直线重合列出等式即可求得b值;(2)利用(1)类似的方法,利用a的表达式来表示b,然后利用导数来研究b的最大值,研究此函数的最值问题,先求出函数的极值,结合函数的单调性,最后确定出最大值与最小值即得.
试题解析:
(1)设![]() 与
与![]() 在公共点
在公共点![]() 处的切线相同
处的切线相同
![]() ,
,
由题意知![]()
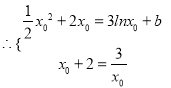 ,
,
由![]() 得,
得, ![]() ,或
,或![]() (舍去)
(舍去)
即有![]() .
.
(2)设![]() 与
与![]() 在公共点
在公共点![]() 处的切线相同
处的切线相同
![]() ,
,
由题意知![]()
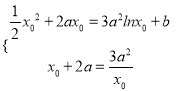 ,
,
由![]() 得,
得, ![]() ,或
,或![]() (舍去),
(舍去),
即有![]() ,
,
令![]() ,则
,则![]() ,
,
于是当![]() ,即
,即![]() 时,
时, ![]() ;
;
当![]() ,即
,即![]() 时,
时, ![]() ,
,
故![]() 在
在![]() 的最大值为
的最大值为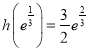 ,故
,故![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
【题目】某老师对全班![]() 名学生学习积极性和参加社团活动情况进行调查,统计数据如下所示:
名学生学习积极性和参加社团活动情况进行调查,统计数据如下所示:
参加社团活动 | 不参加社团活动 | 合计 | |
学习积极性高 |
| ||
学习积极性一般 |
| ||
合计 |
|
|
(1)请把表格数据补充完整;
(2)若从不参加社团活动的![]() 人按照分层抽样的方法选取
人按照分层抽样的方法选取![]() 人,再从所选出的
人,再从所选出的![]() 人中随机选取两人作为代表发言,求至少有一个学习积极性高的概率;
人中随机选取两人作为代表发言,求至少有一个学习积极性高的概率;
(3)运用独立性检验的思想方法分析:请你判断是否有![]() 的把握认为学生的学习积极性与参与社团活动由关系?
的把握认为学生的学习积极性与参与社团活动由关系?
附: 
|
|
|
|
|
|
|
|