题目内容
【题目】在四棱锥P﹣ABCD中， 
=（4，﹣2，3）， 
=（﹣4，1，0）， 
（﹣6，2，﹣8），则该四棱锥的高为 ．
【答案】2
【解析】解：四棱锥P﹣ABCD中， 
=（4，﹣2，3）， 
=（﹣4，1，0）， 
（﹣6，2，﹣8），
设平面ABCD的法向量为 
=（x，y，z），
则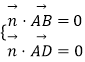 
，
可得 
，
不妨令x=3，则y=12，z=4，
可得 =（3，12，4）；
则 =（﹣6，2，﹣8）在平面ABCD上的射影就是这个四棱锥的高h，
所以h=| ||cos＜ ， ＞|=| 
|= 
=2；
所以该四棱锥的高为2．
所以答案是：2．
【考点精析】解答此题的关键在于理解棱锥的结构特征的相关知识，掌握侧面、对角面都是三角形；平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方．
练习册系列答案
相关题目
【题目】某老师对全班
名学生学习积极性和参加社团活动情况进行调查，统计数据如下所示：
参加社团活动 | 不参加社团活动 | 合计 | |
学习积极性高 |
| ||
学习积极性一般 |
| ||
合计 |
|
|
（1）请把表格数据补充完整；
（2）若从不参加社团活动的
人按照分层抽样的方法选取
人，再从所选出的
人中随机选取两人作为代表发言，求至少有一个学习积极性高的概率；
（3）运用独立性检验的思想方法分析：请你判断是否有
的把握认为学生的学习积极性与参与社团活动由关系？
附： 
|
|
|
|
|
|
|
|
