题目内容
(2011•浙江)已知抛物线C1:x2=y,圆C2:x2+(y﹣4)2=1的圆心为点M
(1)求点M到抛物线C1的准线的距离;
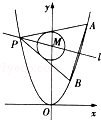
(2)已知点P是抛物线C1上一点(异于原点),过点P作圆C2的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求直线l的方程.
(1)求点M到抛物线C1的准线的距离;
(2)已知点P是抛物线C1上一点(异于原点),过点P作圆C2的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求直线l的方程.

(1)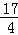 (2)
(2)
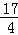 (2)
(2)
(1)由题意画出简图为:
由于抛物线C1:x2=y准线方程为:y=﹣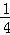 ,圆C2:x2+(y﹣4)2=1的圆心M(0,4),
,圆C2:x2+(y﹣4)2=1的圆心M(0,4),
利用点到直线的距离公式可以得到距离d=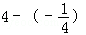 =
=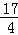 .
.
(2)设点P(x0,x02),A(x1,x12),B(x2,x22);
由题意得:x0≠0,x2≠±1,x1≠x2,
设过点P的圆c2的切线方程为:y﹣x02=k(x﹣x0)即y=kx﹣kx0+x02①
则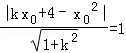 ,即(x02﹣1)k2+2x0(4﹣x02)k+(x02﹣4)2﹣1=0
,即(x02﹣1)k2+2x0(4﹣x02)k+(x02﹣4)2﹣1=0
设PA,PB的斜率为k1,k2(k1≠k2),则k1,k2应该为上述方程的两个根,
∴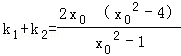 ,
,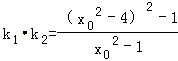 ;
;
代入①得:x2﹣kx+kx0﹣x02="0" 则x1,x2应为此方程的两个根,
故x1=k1﹣x0,x2=k2﹣x0
∴kAB=x1+x2=k1+k2﹣2x0=
由于MP⊥AB,∴kAB•KMP=﹣1⇒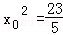
故P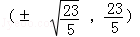 ∴
∴ .
.

由于抛物线C1:x2=y准线方程为:y=﹣
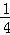 ,圆C2:x2+(y﹣4)2=1的圆心M(0,4),
,圆C2:x2+(y﹣4)2=1的圆心M(0,4),利用点到直线的距离公式可以得到距离d=
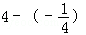 =
=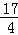 .
.(2)设点P(x0,x02),A(x1,x12),B(x2,x22);
由题意得:x0≠0,x2≠±1,x1≠x2,
设过点P的圆c2的切线方程为:y﹣x02=k(x﹣x0)即y=kx﹣kx0+x02①
则
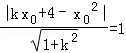 ,即(x02﹣1)k2+2x0(4﹣x02)k+(x02﹣4)2﹣1=0
,即(x02﹣1)k2+2x0(4﹣x02)k+(x02﹣4)2﹣1=0设PA,PB的斜率为k1,k2(k1≠k2),则k1,k2应该为上述方程的两个根,
∴
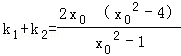 ,
,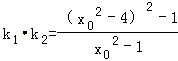 ;
;代入①得:x2﹣kx+kx0﹣x02="0" 则x1,x2应为此方程的两个根,
故x1=k1﹣x0,x2=k2﹣x0
∴kAB=x1+x2=k1+k2﹣2x0=

由于MP⊥AB,∴kAB•KMP=﹣1⇒
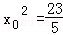
故P
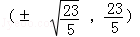 ∴
∴ .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
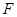
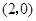 与分别在
与分别在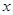 轴、
轴、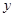 轴上的动点
轴上的动点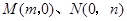 满足:
满足: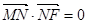 ,动点
,动点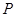 满足
满足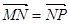 .
.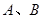 两点,直线
两点,直线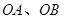 与直线
与直线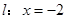 分别交于点
分别交于点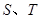 (
(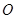 为坐标原点);
为坐标原点);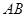 为直径的圆的位置关系;
为直径的圆的位置关系;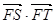 是否为定值?并证明你的结论.
是否为定值?并证明你的结论.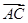 ·
· =0,设P为弦AB的中点.
=0,设P为弦AB的中点.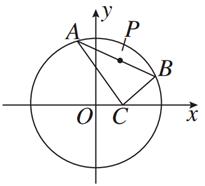
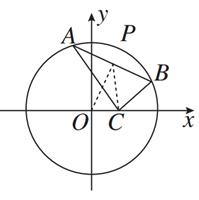
 ,求直线l的方程;
,求直线l的方程;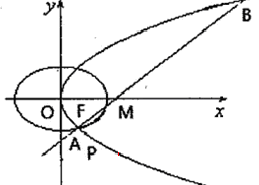
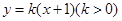 与抛物线
与抛物线 相交于
相交于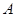 ,
,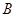 两点,且
两点,且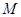 ,
,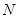 ,若
,若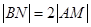 ,则
,则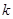 的值是 .
的值是 .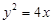 上一点
上一点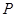 到直线
到直线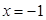 的距离与到点
的距离与到点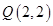 的距离之差的最大值为( )
的距离之差的最大值为( )
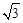
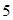

 的焦点作直线交抛物线于
的焦点作直线交抛物线于 两点,线段
两点,线段 的中点
的中点 的纵坐标为2,则线段
的纵坐标为2,则线段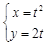 (t为参数)的焦点坐标是 .
(t为参数)的焦点坐标是 .