题目内容
4.已知二次函数f(x)=ax2+bx+c满足:对所有实数x都有f(x+1)-f(x)=2x且f(0)=1.(1)求f(x)的解析式;
(2)求f(x)在[0,2]上的值域.
分析 (1)二次函数f(x)=ax2+bx+c代入f(x+1)-f(x)=2x,根据系数对应相等可求a,b,而f(0)=1,进而可求f(x);
(2)利用配方法,结合函数的单调性,即可求f(x)在[0,2]上的值域.
解答 解:(1):∵f(x)=ax2+bx+c,
∴f(x+1)-f(x)=a(x+1)2+b(x+1)+c-(ax2+bx+c)=2ax+a+b=2x,
∴$\left\{\begin{array}{l}{2a=2}\\{a+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=1}\\{b=-1}\end{array}\right.$,即f(x)=x2-x+c,
又∵f(0)=1,
∴c=1,则f(x)=x2-x+1;
(2)f(x)=x2-x+1=(x-$\frac{1}{2}$)2+$\frac{3}{4}$,
∴函数在[0,$\frac{1}{2}$]上单调递减,在[$\frac{1}{2}$,2]上单调递增,
∴f(x)min=$\frac{3}{4}$,f(x)max=3,
∴$f(x)在[0,2]上的值域为[\frac{3}{4},3]$.
点评 本题主要考查了利用待定系数法求解二次函数的解析式,以及函数的恒成立与函数的最值求解的相互转化,主要涉及单调性在函数的最值求解中的应用.属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知函数f(x)=2sin2x+2$\sqrt{3}$sinxcosx-1的图象关于(φ,0)对称,则φ的值可以是( )
| A. | $-\frac{π}{6}$ | B. | $\frac{π}{6}$ | C. | $-\frac{π}{12}$ | D. | $\frac{7π}{12}$ |
9.若向量$\overrightarrow a$=(1,2),$\overrightarrow{b}$=(1,-1),则2$\overrightarrow a$+$\overrightarrow{b}$与$\overrightarrow a$-$\overrightarrow{b}$的夹角等于( )
| A. | -$\frac{π}{4}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{3π}{4}$ |
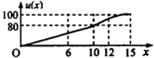
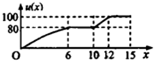
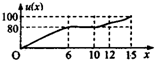
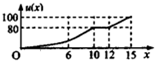
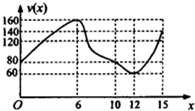 一辆赛车在跑道上高速行驶,如图反映了它从某时刻开始的15分钟内速度v(x)与时间x的关系,若定义“速度差函数”u(x)为时间段[0,x]内的最大速度与最小速度的差,则u(x)的图象可能是( )
一辆赛车在跑道上高速行驶,如图反映了它从某时刻开始的15分钟内速度v(x)与时间x的关系,若定义“速度差函数”u(x)为时间段[0,x]内的最大速度与最小速度的差,则u(x)的图象可能是( )