题目内容
9.若向量$\overrightarrow a$=(1,2),$\overrightarrow{b}$=(1,-1),则2$\overrightarrow a$+$\overrightarrow{b}$与$\overrightarrow a$-$\overrightarrow{b}$的夹角等于( )| A. | -$\frac{π}{4}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{3π}{4}$ |
分析 由已知中向量$\overrightarrow a$=(1,2),$\overrightarrow{b}$=(1,-1),我们可以计算出2$\overrightarrow a$+$\overrightarrow{b}$与$\overrightarrow a$-$\overrightarrow{b}$的坐标,代入向量夹角公式即可得到答案.
解答 解:∵$\overrightarrow a$=(1,2),$\overrightarrow{b}$=(1,-1),
∴2$\overrightarrow a$+$\overrightarrow{b}$=2(1,2)+(1,-1)=(3,3),
$\overrightarrow a$-$\overrightarrow{b}$=(1,2)-(1,-1)=(0,3),
∴(2$\overrightarrow a$+$\overrightarrow{b}$)($\overrightarrow a$-$\overrightarrow{b}$)=0×3+3×9=9,
|2$\overrightarrow a$+$\overrightarrow{b}$|=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,|$\overrightarrow a$-$\overrightarrow{b}$|=3,
∴cosθ=$\frac{9}{3\sqrt{2}•3}$=$\frac{\sqrt{2}}{2}$,
∵0≤θ≤π,
∴θ=$\frac{π}{4}$
故选:C
点评 本题考查的知识点是数量积表示两个向量的夹角,其中利用公式,是利用向量求夹角的最常用的方法,一定要熟练掌握.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
6.在($\sqrt{x}-\frac{2}{\sqrt{x}}$)n的展开式中,偶数项的二次项系数为64,则展开式共有( )
| A. | 6项 | B. | 7项 | C. | 8项 | D. | 9项 |
20.经过A(-2,0),B(-5,3)两点的直线的倾斜角( )
| A. | 45° | B. | 135° | C. | 90° | D. | 60° |
17.若tanθ=2,则sin2θ+sinθcosθ-2cos2θ=( )
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{\sqrt{7}}{4}$ | D. | $\frac{3}{4}$ |
19.下面说法错误的是( )
| A. | 数乘向量就是一个实数λ与向量$\overrightarrow{a}$的乘积 | |
| B. | λ>0,λ$\overrightarrow{a}$就是把$\overrightarrow{a}$同方向放大或缩小 | |
| C. | λ$\overrightarrow{a}$就是把$\overrightarrow{a}$沿反方向放大或缩小 | |
| D. | λ=0,则$λ\overrightarrow{a}$=$\overrightarrow{0}$ |
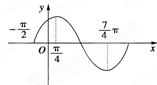 函数f(x)=sin(ωx+φ),(|φ|<$\frac{π}{2}$)的图象如图所示.试求:
函数f(x)=sin(ωx+φ),(|φ|<$\frac{π}{2}$)的图象如图所示.试求: