题目内容
13.已知tanx=2,求下列各式的值:(1)$\frac{cosx+sinx}{cosx-sinx}$;
(2)cos2x-sin2x;
(3)3sinxcosx.
分析 转化所求表达式为正切函数的形式,然后代入求解即可.
解答 解:tanx=2,
(1)$\frac{cosx+sinx}{cosx-sinx}$=$\frac{1+tanx}{1-tanx}$=$\frac{1+2}{1-2}$=-3;
(2)cos2x-sin2x=$\frac{{cos}^{2}α-{sin}^{2}α}{{cos}^{2}α+{sin}^{2}α}$=$\frac{1-{tan}^{2}α}{1+{tan}^{2}α}$=$\frac{1-4}{1+4}$=-$\frac{3}{5}$;
(3)3sinxcosx=$\frac{3sinαcosα}{{cos}^{2}α+{sin}^{2}α}$=$\frac{3tanα}{1+{tan}^{2}α}$=$\frac{3×2}{1+4}$=$\frac{6}{5}$.
点评 本题考查三角函数的化简求值,同角三角函数的基本关系式的应用,考查计算能力.

练习册系列答案
相关题目
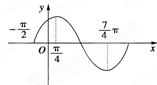 函数f(x)=sin(ωx+φ),(|φ|<$\frac{π}{2}$)的图象如图所示.试求:
函数f(x)=sin(ωx+φ),(|φ|<$\frac{π}{2}$)的图象如图所示.试求: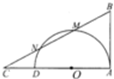 如图,已知AD为半圆O的直径,AB为半圆O的切线,割线BMN交AD的延长线于点C,且BM=MN=NC,AB=2$\sqrt{2}$.
如图,已知AD为半圆O的直径,AB为半圆O的切线,割线BMN交AD的延长线于点C,且BM=MN=NC,AB=2$\sqrt{2}$.