题目内容
若圆
上有且只有两个点到直线
的距离等于1，则半径
的取值范围是( )
| A．（0, 2） | B．（1, 2） | C．（1, 3） | D．（2, 3） |
C
解析试题分析：设圆心（3，-5）到直线4x-3y=17的距离为d，则由题意可得r-1＜d＜r+1，利用点到直线的距离公式求出d的值，解不等式求得半径r的取值范围.即为
，故选C.
考点：直线和圆的位置关系
点评:本题主要考查直线和圆的位置关系，点到直线的距离公式，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
表示一个圆，则
的取值范围是( )
| A．≤2 | B． | C． | D．≤ |
若直线x－y＝2被圆(x－a)2＋y2＝4所截得的弦长为2
，则实数a的值为
A．－1或 | B．1或3 | C．－2或6 | D．0或4 |
过点
作圆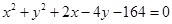
的弦，其中弦长为整数的共有（ ）
| A．16条 | B．17条 | C．32条 | D．34条 |
若方程
表示圆，则
的取值范围是（ ）
A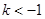． | B． | C． | D． |
直线
截圆
所得劣弧所对的圆心角是
A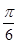． | B． |
C． | D． |
若直线
与圆
有公共点，则实数
取值范围是 （ ）
A． | B． | C．  | D． |
圆
关于直线
对称的圆的方程是（ ）
A． | B． |
C． | D． |
已知圆的方程为
.设该圆过点（3，5）的两条弦分别为AC和BD，且
.则四边形ABCD的面积最大值为（ ）
A．20 | B．30 | C．49 | D．50 |