题目内容
过点 作圆
作圆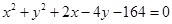 的弦,其中弦长为整数的共有( )
的弦,其中弦长为整数的共有( )
| A.16条 | B.17条 | C.32条 | D.34条 |
C.
解析试题分析:圆的标准方程是:(x+1)2+(y-2)2=132,圆心(-1,2),半径r=13过点A(11,2)的最短的弦长为10,最长的弦长为26,(分别只有一条)还有长度为11,12,…,25的各2条,所以共有弦长为整数的2+2×15=32条.
故选C.
考点:本题主要考查圆的方程及其的弦长问题。
点评:易错题,实际上是求弦长问题,容易遗漏“除最小最大弦长外,各有2条”。

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
在圆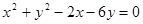 内,过点
内,过点 的最长弦和最短弦分别是AC和BD,则四边形ABCD的面积为
的最长弦和最短弦分别是AC和BD,则四边形ABCD的面积为
A.5 | B.10 | C.15 | D.20 |
已知点 内任意一点,点
内任意一点,点 是圆上任意一点,则实数
是圆上任意一点,则实数 ( )
( )
| A.一定是负数 | B.一定等于0 |
| C.一定是正数 | D.可能为正数也可能为负数 |
若函数 的图象在
的图象在 处的切线
处的切线 与圆
与圆 相离,则点
相离,则点 与圆C的位置关系是 ( )
与圆C的位置关系是 ( )
| A.点在圆外 | B.点在圆内 | C.点在圆上 | D.不能确定 |
若直线 经过点
经过点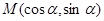 ,则 ( )
,则 ( )
A. . . | B. . . |
C. . . | D. . . |
若圆 上有且只有两个点到直线
上有且只有两个点到直线 的距离等于1,则半径
的距离等于1,则半径 的取值范围是( )
的取值范围是( )
| A.(0, 2) | B.(1, 2) | C.(1, 3) | D.(2, 3) |
若直线 过圆
过圆 的圆心,则
的圆心,则 的值为( )
的值为( )
A. | B. | C. | D. |
圆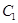 :
:  与圆
与圆 :
:  的位置关系是
的位置关系是
| A.外离 | B.相交 | C.内切 | D.外切 |
 中,圆
中,圆 的方程为
的方程为 ,若直线
,若直线 上至少存在一点,使得以该点为圆心,1为半径的圆与圆
上至少存在一点,使得以该点为圆心,1为半径的圆与圆 的取值范围是( )
的取值范围是( )
 或
或
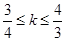
 或
或