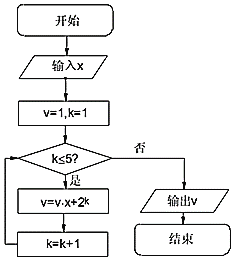
题目内容
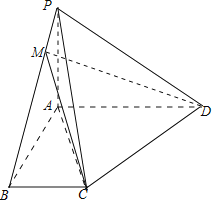
【题目】如图,四棱锥P﹣ABCD中,已知PA⊥平面ABCD,△ABC为等边三角形,PA=2AB=2,AC⊥CD,PD与平面PAC所成角的余弦值为![]() .
.
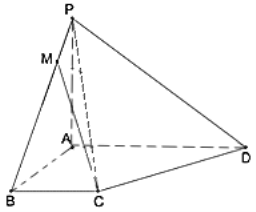
(1)证明:![]() 平面PAD;
平面PAD;
(2)点M为PB上一点,且![]() ,试判断点M的位置.
,试判断点M的位置.
【答案】(1)证明见解析.(2)点M的位置是靠近P的四等分点.
【解析】
(1)由PA⊥平面ABCD,得PA⊥CD,求解三角形证明∠CAD=60°,结合∠BCA=60°,得到BC∥AD,由直线与平面平行的判定可得BC∥平面PAD;
(2)设![]() ,则VM﹣PCD=λVB﹣PCD=λVP﹣BCD,求出三棱锥P﹣BCD的体积,结合
,则VM﹣PCD=λVB﹣PCD=λVP﹣BCD,求出三棱锥P﹣BCD的体积,结合![]() 求得λ值,可得点M的位置.
求得λ值,可得点M的位置.
(1)证明:∵PA⊥平面ABCD,∴PA⊥CD,
又AC⊥CD,CA∩PA=A,∴CD⊥平面PAC,
∴PD与平面PAC所成角为∠DPC,
在Rt△PCD中,cos∠DPC![]() ,
,
在Rt△PAC中,∵PC![]() ,∴PD=2
,∴PD=2![]() ,
,
在Rt△PAD中,∵PA=2,∴AD=2,
在Rt△ACD中,求得∠CAD=60°.
又∠BCA=60°,∴在平面ABCD中,得到BC∥AD,
而AD平面PAD,BC平面PAD,
∴BC∥平面PAD;
(2)解:∵点M在PB上,设![]() .
.
则VM﹣PCD=λVB﹣PCD=λVP﹣BCD,
∵![]() ,
,
∴![]() ,得
,得![]() .
.
∴点M的位置是靠近P的四等分点.

 阅读快车系列答案
阅读快车系列答案【题目】某校高一、高二年级的全体学生都参加了体质健康测试,测试成绩满分为![]() 分,规定测试成绩在
分,规定测试成绩在![]() 之间为“体质优秀”,在
之间为“体质优秀”,在![]() 之间为“体质良好”,在
之间为“体质良好”,在![]() 之间为“体质合格”,在
之间为“体质合格”,在![]() 之间为“体质不合格”.现从这两个年级中各随机抽取
之间为“体质不合格”.现从这两个年级中各随机抽取![]() 名学生,测试成绩如下:
名学生,测试成绩如下:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
高一年级 | 60 | 85 | 80 | 65 | 90 | 91 | 75 |
高二年级 | 79 | 85 | 91 | 75 | 60 |
|
|
其中![]() 是正整数.
是正整数.
(1)若该校高一年级有![]() 学生,试估计高一年级“体质优秀”的学生人数;
学生,试估计高一年级“体质优秀”的学生人数;
(2)若从高一年级抽取的![]() 名学生中随机抽取
名学生中随机抽取![]() 人,记
人,记![]() 为抽取的
为抽取的![]() 人中为“体质良好”的学生人数,求
人中为“体质良好”的学生人数,求![]() 的分布列及数学期望;
的分布列及数学期望;
(3)设两个年级被抽取学生的测试成绩的平均数相等,当高二年级被抽取学生的测试成绩的方差最小时,写出![]() 的值.(只需写出结论)
的值.(只需写出结论)
【题目】近年来,国家相关政策大力鼓励创新创业种植业户小李便是受益者之一,自从2017年毕业以来,其通过自主创业而种植的某种农产品广受市场青睐,他的种植基地也相应地新增加了一个平时小李便带着部分员工往返于新旧基地之间进行科学管理和经验交流,新旧基地之间开车单程所需时间为![]() ,由于不同时间段车流量的影响,现对50名员工往返新旧基地之间的用时情况进行统计,结果如下:
,由于不同时间段车流量的影响,现对50名员工往返新旧基地之间的用时情况进行统计,结果如下:
| 30 | 35 | 40 | 45 | 50 |
频数(人) | 10 | 20 | 10 | 5 | 5 |
(1)若有50名员工参与调查,现从单程时间在35分钟,40分钟,45分钟的人员中按分层抽样的方法抽取7人,再从这7人中随机抽取3人进行座谈,用![]() 表示抽取的3人中时间在40分钟的人数,求
表示抽取的3人中时间在40分钟的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)某天,小李需要从旧基地驾车赶往新基地召开一个20分钟的紧急会议,结束后立即返回旧基地.(以50名员工往返新旧基地之间的用时的频率作为用时发生的概率)
①求小李从离开旧基地到返回旧基地共用时间不超过110分钟的概率;
②若用随机抽样的方法从旧基地抽取8名骨干员工陪同小李前往新基地参加此次会议,其中有![]() 名员工从离开旧基地到返回旧基地共用时间不超过110分钟,求随机变量
名员工从离开旧基地到返回旧基地共用时间不超过110分钟,求随机变量![]() 的方差.
的方差.