题目内容
20.已知函数f(x)=alnx+$\frac{a}{2}$x2+x,g(x)=$\frac{a-2}{2}$x2+(a+1)x+$\frac{a+2}{2}$;(1)若f(x)在(1,f(1))处的切线方程为x+y+b=0,求a,b的值;
(2)是否存在实数a使得f(x)在(0,+∞)上单调递减,g(x)在(0,$\frac{1}{5}$)上单调递增,若存在,求出a的值,若不存在,请说明理由.
(3)令H(x)=f(x+1)-g(x),若x1,x2(x1<x2)是H(x)的两个极值点,证明:(-$\frac{1}{2}$+ln2)x1<H(x2)<0.
分析 (1)求出导数,由切线方程可得f′(1)=-1,可得a=-1,求得切点,代入切线方程,可得b;
(2)假设存在符合条件的a值,运用参数分离和基本不等式可得a的范围,结合单调性和导数的关系,可得a的值;
(3)化简H(x)的解析式,求出导数,结合二次方程的韦达定理,可得H(x2)<0成立;再由分析法,结合函数的单调性,证明(-$\frac{1}{2}$+ln2)x1<H(x2).
解答  解:(1)f′(x)=$\frac{a}{x}$+ax+1,
解:(1)f′(x)=$\frac{a}{x}$+ax+1,
由题意:f′(1)=-1即2a+1=-1,∴a=-1,
即f(x)=-lnx-$\frac{1}{2}$x2+x,
由f(1)=$\frac{3}{2}$,切点(1,$\frac{1}{2}$)在切线上∴b=-$\frac{3}{2}$;
(2)∵f(x)在(0,+∞)上单调递减,
∴f′(x)=$\frac{a}{x}$+ax+1≤0在x∈(0,+∞)时恒成立,
即a≤-$\frac{1}{x+\frac{1}{x}}$在x∈(0,+∞)时恒成立,
∵x+$\frac{1}{x}$≥2∴0<$\frac{1}{x+\frac{1}{x}}$≤$\frac{1}{2}$∴-$\frac{1}{x+\frac{1}{x}}$∈[-$\frac{1}{2}$,0),
∴a≤-$\frac{1}{2}$
∵假设存在符合条件的a值,则应有:a≤-$\frac{1}{2}$∴$\frac{a-2}{2}$<0
此时g(x)的对称轴为:x=-$\frac{a+1}{a-2}$,
若使g(x)在(0,$\frac{1}{5}$)上单调递增,应有:-$\frac{a+1}{a-2}$≥$\frac{1}{5}$
解得:a≥-$\frac{1}{2}$,
综上,存在实数a=-$\frac{1}{2}$使得f(x)在(0,+∞)上单调递减,g(x)在(0,$\frac{1}{5}$ )上单调递增.
(3)证明:H(x)=f(x+1)-g(x)=aln(x+1)+$\frac{a}{2}$ (x+1)2+(x+1)-$\frac{a-2}{2}$ x2-(a+1)x-$\frac{a+2}{2}$
=aln(x+1)+x2
H′(x)=$\frac{a}{x+1}$+2x=$\frac{2{x}^{2}+2x+a}{x+1}$,
由题意:2x2+2x+a=0在区间(-1,+∞)内有两个不等实根x1,x2
记G(x)=2x2+2x+a 则应有:△>0,G(-1)>0,解得:0<a<$\frac{1}{2}$;
由韦达定理得:x1+x2=-1,x1•x2=$\frac{a}{2}$
∴x1=-x2-1,a=2x1•x2=-2(x2+1)x2
x1∈(-1,-$\frac{1}{2}$),x2∈(-$\frac{1}{2}$,0),
H(x)在(-1,x1)上单调递增,在(x1,x2)上单调递减,在(x2,+∞)上单调递增
∵x2<0,∴H(x2)<H(0)=0
即H(x2)<0成立;
下面证明:H(x2)>(-$\frac{1}{2}$+ln2)x1
∵H(x2)=aln(x2+1)+x22=-2(x2+1)x2ln(x2+1)+x22
(-$\frac{1}{2}$+ln2)x1=(-$\frac{1}{2}$+ln2)(-1-x2),
∴只需证明:-2(x2+1)x2ln(x2+1)+x22>(-$\frac{1}{2}$+ln2)(-1-x2)
即:x22-2(x2+1)x2ln(x2+1)+(ln2-$\frac{1}{2}$)x2>$\frac{1}{2}$-ln2…①
令ϕ(x)=x2-2(x+1)xln(x+1)+(ln2-$\frac{1}{2}$)x,x∈(-$\frac{1}{2}$,0),
ϕ′(x)=2x-2(2x+1)ln(x+1)-2x+ln2-$\frac{1}{2}$=-2(2x+1)ln(x+1)+ln2-$\frac{1}{2}$,
∵-$\frac{1}{2}$<x<0∴x+1<1,ln(x+1)<0,
2x+1>0∴-2(2x+1)ln(x+1)>0,
又∵ln2-$\frac{1}{2}$=ln2-ln$\sqrt{e}$=ln$\sqrt{\frac{4}{e}}$>0,∴ϕ′(x)>0,
∴ϕ(x)在(-$\frac{1}{2}$,0)上单调递增
∴ϕ(x)>ϕ(-$\frac{1}{2}$)=$\frac{1}{4}$-$\frac{1}{2}$ln2-$\frac{1}{2}$ln2+$\frac{1}{4}$=$\frac{1}{2}$-ln2,
即ϕ(x)>$\frac{1}{2}$-ln2 即①式成立
∴H(x2)>(-$\frac{1}{2}$+ln2)x1
综上:(-$\frac{1}{2}$+ln2)x1<H(x2)<0成立.
点评 本题考查导数的运用:求切线的方程和单调区间、极值和最值,同时考查不等式恒成立思想转化为求函数的最值,以及函数单调性的运用和二次方程韦达定理,考查运算求解能力,属于难题.

| A. | (-∞,$\frac{1}{\sqrt{e}}$) | B. | (-$\sqrt{e}$,$\frac{1}{\sqrt{e}}$) | C. | (-$\frac{1}{\sqrt{e}}$,$\sqrt{e}$) | D. | (0,$\sqrt{e}$) |
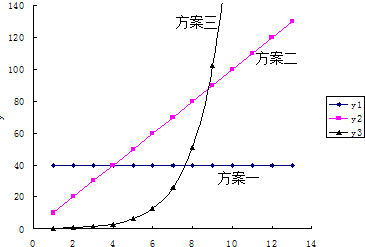
| A. | 投资3天以内(含3天),采用方案一 | B. | 投资4天,不采用方案三 | ||
| C. | 投资6天,采用方案二 | D. | 投资10天,采用方案二 |
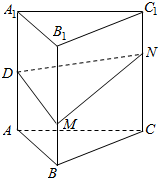 如图,正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)的各条棱长均相等,D为AA1的中点.M、N分别是BB1、CC1上的动点(含端点),且满足BM=C1N.当M,N运动时,下列结论中不正确的是( )
如图,正三棱柱ABC-A1B1C1(底面是正三角形,侧棱垂直底面)的各条棱长均相等,D为AA1的中点.M、N分别是BB1、CC1上的动点(含端点),且满足BM=C1N.当M,N运动时,下列结论中不正确的是( )| A. | 平面DMN⊥平面BCC1B1 | |
| B. | 三棱锥A1-DMN的体积为定值 | |
| C. | △DMN可能为直角三角形 | |
| D. | 平面DMN与平面ABC所成的锐二面角范围为(0,$\frac{π}{4}$] |