题目内容
(12分)设直线 与椭圆
与椭圆 相切。 (I)试将
相切。 (I)试将 用
用 表示出来; (Ⅱ)若经过动点
表示出来; (Ⅱ)若经过动点 可以向椭圆引两条互相垂直的切线,
可以向椭圆引两条互相垂直的切线, 为坐标原点,求证:
为坐标原点,求证: 为定值。
为定值。
 与椭圆
与椭圆 相切。 (I)试将
相切。 (I)试将 用
用 表示出来; (Ⅱ)若经过动点
表示出来; (Ⅱ)若经过动点 可以向椭圆引两条互相垂直的切线,
可以向椭圆引两条互相垂直的切线, 为坐标原点,求证:
为坐标原点,求证: 为定值。
为定值。(Ⅰ)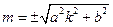 (Ⅱ)
(Ⅱ) 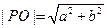
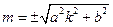 (Ⅱ)
(Ⅱ) 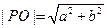
(I)将 代入
代入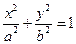 得
得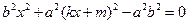 ,整理得
,整理得
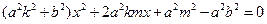
由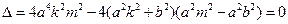 得
得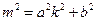 ,故
,故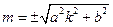
(Ⅱ)当两条切线的斜率都存在而且不等于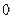 时,设其中一条的斜率为k,
时,设其中一条的斜率为k,
则另外一条的斜率为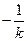 于是由上述结论可知椭圆斜率为k的切线方程为
于是由上述结论可知椭圆斜率为k的切线方程为
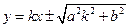 ① 又椭圆斜率为
① 又椭圆斜率为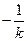 的切线方程为
的切线方程为
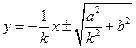 ② 由①得
② 由①得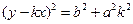
由②得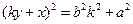 两式相加得
两式相加得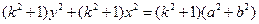
于是,所求P点坐标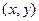 满足
满足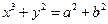
因此,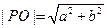 当一条切线的斜率不存在时,另一条切线的斜率必为0,此时显然也有
当一条切线的斜率不存在时,另一条切线的斜率必为0,此时显然也有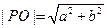 所以
所以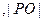 为定值。
为定值。
 代入
代入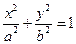 得
得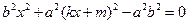 ,整理得
,整理得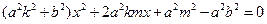
由
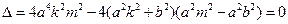 得
得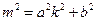 ,故
,故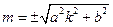
(Ⅱ)当两条切线的斜率都存在而且不等于
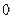 时,设其中一条的斜率为k,
时,设其中一条的斜率为k,则另外一条的斜率为
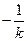 于是由上述结论可知椭圆斜率为k的切线方程为
于是由上述结论可知椭圆斜率为k的切线方程为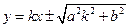 ① 又椭圆斜率为
① 又椭圆斜率为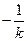 的切线方程为
的切线方程为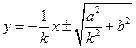 ② 由①得
② 由①得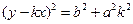
由②得
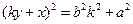 两式相加得
两式相加得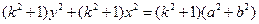
于是,所求P点坐标
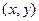 满足
满足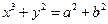
因此,
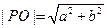 当一条切线的斜率不存在时,另一条切线的斜率必为0,此时显然也有
当一条切线的斜率不存在时,另一条切线的斜率必为0,此时显然也有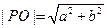 所以
所以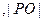 为定值。
为定值。
练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目

 的离心率为
的离心率为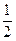 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线 相切.
相切. 的方程;
的方程; ,
, ,
, 是椭圆
是椭圆 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结 交椭圆
交椭圆 ,证明直线
,证明直线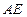 与
与 ;
; ,
, 两点,求
两点,求 的取值范围.
的取值范围.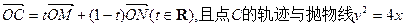 交于A、B两点。
交于A、B两点。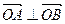 ;
;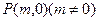 ,使得过点P的直线l交抛物线
,使得过点P的直线l交抛物线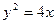 于D、E两点,并以线段DE为直径的圆都过原点。若存在,请求出m的值,若不存在,请说明理由。
于D、E两点,并以线段DE为直径的圆都过原点。若存在,请求出m的值,若不存在,请说明理由。 ,则当
,则当 取最小值时,椭圆
取最小值时,椭圆 的离心率是( )
的离心率是( )



 中,
中, ,且
,且 。现建立以A点为坐标原点,以
。现建立以A点为坐标原点,以 的平分线所在直线为x轴的平面直角坐标系,如图所示。
的平分线所在直线为x轴的平面直角坐标系,如图所示。 的值。
的值。
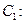
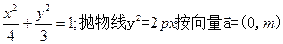
 ,
,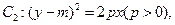 且
且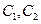 的公共弦
的公共弦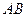 过椭圆
过椭圆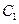 的右焦点。
的右焦点。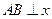 轴时,求
轴时,求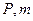 的值,并判断抛物线
的值,并判断抛物线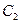 的焦点是否在直线
的焦点是否在直线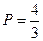 ,且抛物线
,且抛物线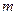 的值及直线AB的方程。
的值及直线AB的方程。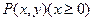 到定点
到定点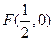 的距离比它到
的距离比它到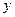 轴的距离大
轴的距离大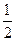 .记点
.记点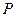 的轨迹为曲线
的轨迹为曲线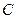
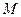 过
过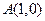 ,且圆心
,且圆心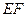 是圆
是圆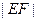 是否为定值?请说明理由.
是否为定值?请说明理由.