Question

【题目】设定义在R上的函数f（x）是最小正周期2π的偶函数，f′（x）是函数f（x）的导函数，当x∈[0，π]时，0＜f（x）＜1；当x∈（0，π），且x≠ 时，（x﹣ ）f′（x）＞0，则函数y=f（x）﹣sinx在[﹣2π，2π]上的零点个数为（ ）
A.2
B.4
C.5
D.8

Answer 1

【答案】B
【解析】解：∵x∈（0，π），且x≠ 时，（x﹣ ）f′（x）＞0， ∴x∈（0， ），函数单调减，x∈（ ，π），函数单调增，
∵x∈[0，π]时，0＜f（x）＜1，
在R上的函数f（x）是最小正周期为2π的偶函数，在同一坐标系中作出y=sinx和y=f（x）草图像如下，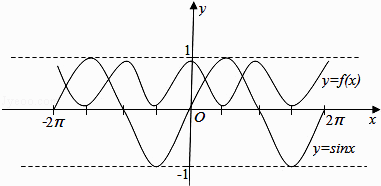

由图知y=f（x）﹣sinx在[﹣2π，2π]上的零点个数为4个．
故选：B．