题目内容
【题目】如图,已知F为抛物线y2=4x的焦点,点A,B,C在该抛物线上,其中A,C关于x轴对称(A在第一象限),且直线BC经过点F. 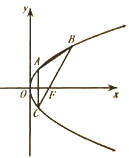
(1)若△ABC的重心为G( ![]() ),求直线AB的方程;
),求直线AB的方程;
(2)设S△ABO=S1 , S△CFO=S2 , 其中O为坐标原点,求S12+S22的最小值.
【答案】
(1)解:设A(x1,y1),B(x2,y2),C(x1,﹣y1),
则△ABC的重心坐标为G( ![]() ,
, ![]() ),
),
由题意可得2x1+x2= ![]() ,且y2=4,
,且y2=4,
由y22=4x2,y12=4x1,
可得x2=4,y2=4,和x1= ![]() ,y1=1,
,y1=1,
直线AB的斜率k= ![]() =
= ![]() ,
,
即有直线AB的方程为4x﹣5y+4=0;
(2)解:设A(x1,y1),B(x2,y2),C(x1,﹣y1),
设直线BC:x=my+1,代入抛物线方程y2=4x,可得
y2﹣4my﹣4=0,可得﹣y1y2=﹣4,即y1y2=4,
再设直线AB:y=kx+n,代入抛物线方程,可得
ky2﹣4y+4n=0,y1y2= ![]() =4,即n=k,
=4,即n=k,
则有直线AB:y=k(x+1),即有直线AB恒过定点E(﹣1,0),
则S△ABO= ![]() |OE||y2﹣y1|=
|OE||y2﹣y1|= ![]() |y2﹣y1|,
|y2﹣y1|,
S△CFO= ![]() |OF||y1|=
|OF||y1|= ![]() |y1|,
|y1|,
即有S12+S22= ![]() (y2﹣y1)2+
(y2﹣y1)2+ ![]() y12=
y12= ![]() =
= ![]() (2y12+
(2y12+ ![]() ﹣8)
﹣8)
≥ ![]() (2
(2 ![]() ﹣8)=2
﹣8)=2 ![]() ﹣2.
﹣2.
即有S12+S22的最小值为2 ![]()
![]() ,y2=
,y2= ![]()
【解析】(1)设A(x1 , y1),B(x2 , y2),C(x1 , ﹣y1),运用三角形的重心坐标公式和抛物线方程,即可求得A,B的坐标,进而得到直线方程;(2)通过直线BC,AB的方程和抛物线方程,运用韦达定理,可得恒过定点(﹣1,0),即有S△ABO= ![]() |OE||y2﹣y1|=
|OE||y2﹣y1|= ![]() |y2﹣y1|,S△CFO=
|y2﹣y1|,S△CFO= ![]() |OF||y1|=
|OF||y1|= ![]() |y1|,y1y2=4,再由基本不等式计算即可得到最小值.
|y1|,y1y2=4,再由基本不等式计算即可得到最小值.