题目内容
【题目】某学校对甲、乙两个班级进行了物理测验，成绩统计如下（每班50人）：
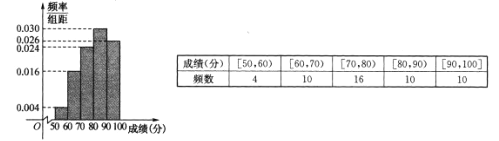
（1）估计甲班的平均成绩；
（2）成绩不低于80分记为“优秀”.请完成下面的
列联表，并判断是否有85%的把握认为：“成绩优秀”与所在教学班级有关？
（3）从两个班级，成绩在
的学生中任选2人，记事件
为“选出的2人中恰有1人来自甲班”.求事件
的概率
.
附：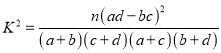 
【答案】（1）80.8；（2）有85%的把握认为“成绩优秀”与所在教学班级有关；（3）
．
【解析】试题分析：（1）在频率分布直方图中，平均数的计算方法：每个小矩形的面积乘以小矩形底边中点的横坐标之和，算出甲班的成绩；（2）利用已知图形完成列联表，算出卡方约等于
，故 85%的把握认为“成绩优秀”与所在教学班级有关；（3）采用列举法求出事件A的概率。
试题解析：（1）估计，甲班的平均成绩为：
.
（2）
列联表如下：
成绩优秀 | 成绩不优秀 | 总计 | |
甲班 | 28 | 22 | 50 |
乙班 | 20 | 30 | 50 |
总计 | 48 | 52 | 100 |
.
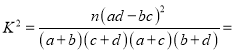
有85%的把握认为“成绩优秀”与所在教学班级有关.
（3）成绩在内，甲班的2人分别记为
， 
；乙班的4人分别记为
， 
， 
， 
总的基本事件有：
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
，共15个.
其中事件包含的基本事件有： 
， 
， 
， 
， 
， 
， 
， 
，共8个.
所以
.
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度，现在某市进行调查，随机抽调了50人，他们年龄的频数分布及支持“生育二胎”人数如下表：
年龄 | [5，15） | [15，25） | [25，35） | [35，45） | [45，55） | [55，65） |
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
（1）由以上统计数据填下面2×2列联表；
年龄不低于45岁的人 | 年龄低于45岁的人 | 合计 | |
支持“生育二胎” | a= | c= | |
不支持“生育二胎” | b= | d= | |
合计 |
（2）判断是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异．
P（K2≥k） | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
附表：K2= 
．
