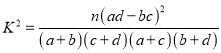ĢāÄæÄŚČŻ
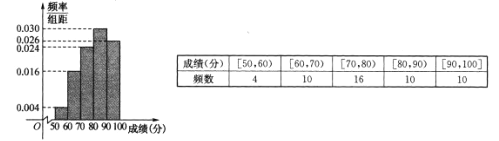
”¾ĢāÄæ”æ¼×”¢ŅŅĮ½ĆūŌĖ¶ÆŌ±²Ī¼Ó”°Ń”°Ī²āŹŌČü”±£¬ŌŚĻąĶ¬Ģõ¼žĻĀ£¬Į½ČĖ6“Ī²āŹŌµÄ³É¼Ø£Øµ„Ī»£ŗ·Ö£©¼ĒĀ¼ČēĻĀ£ŗ
¼× 86 77 92 72 78 84
ŅŅ 78 82 88 82 95 90
£Ø1£©ÓĆ¾„Ņ¶Ķ¼±ķŹ¾ÕāĮ½×鏿¾Ż£¬ĻÖŅŖ“ÓÖŠŃ”ÅÉŅ»ĆūŌĖ¶ÆŌ±²Ī¼Ó±ČČü£¬ÄćČĻĪŖŃ”ÅÉĖ²ĪČüøüŗĆ£æĖµĆ÷ĄķÓɣز»ÓĆ¼ĘĖć£©£»
£Ø2£©Čō½«ĘµĀŹŹÓĪŖøÅĀŹ£¬¶ŌŌĖ¶ÆŌ±¼×ŌŚ½ńŗóČż“Ī²āŹŌ³É¼Ø½ųŠŠŌ¤²ā£¬¼ĒÕāČż“Ī³É¼ØøßÓŚ85·ÖµÄ“ĪŹżĪŖ![]() £¬Ēó
£¬Ēó![]() µÄ·Ö²¼ĮŠŗĶŹżŃ§ĘŚĶū
µÄ·Ö²¼ĮŠŗĶŹżŃ§ĘŚĶū![]() ¼°·½²ī
¼°·½²ī![]() .
.
”¾“š°ø”æ(1) ¹ŹŃ”ŅŅ£»(2) ![]() £¬
£¬ ![]() .
.
”¾½āĪö”æŹŌĢā·ÖĪö£ŗ£Ø1£©øł¾Ż¾„Ņ¶Ķ¼µÄ¶ØŅ壬¹Ū²ģŹż¾ŻµÄĘ½¾łÖµŅŌ¼°Źż¾Ż·ÖÉ¢Óė¼ÆÖŠ³Ģ¶ČæÉµĆ½į¹ū£»£Ø2£©¼×ŌĖ¶ÆŌ±Ćæ“Ī²āŹŌøßÓŚ85·ÖµÄøÅĀŹ“óŌ¼ŹĒ![]() £¬³É¼ØøßÓŚ85·ÖµÄ“ĪŹżĪŖ
£¬³É¼ØøßÓŚ85·ÖµÄ“ĪŹżĪŖ![]() ·ž“Ó¶žĻī·Ö²¼£¬“Ó¶ųæÉµĆ·Ö²¼ĮŠ£¬ĄūÓƶžĻī·Ö²¼µÄĘŚĶūÓė·½²ī¹«Ź½æÉµĆ½į¹ū.
·ž“Ó¶žĻī·Ö²¼£¬“Ó¶ųæÉµĆ·Ö²¼ĮŠ£¬ĄūÓƶžĻī·Ö²¼µÄĘŚĶūÓė·½²ī¹«Ź½æÉµĆ½į¹ū.
ŹŌĢā½āĪö£ŗ£Ø1£©
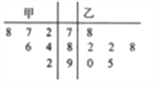
ÓÉĶ¼æÉÖŖŅŅµÄĘ½¾łĖ®Ę½±Č¼×øߣ¬¹ŹŃ”ŅŅ£®
£Ø2£©¼×ŌĖ¶ÆŌ±Ćæ“Ī²āŹŌøßÓŚ85·ÖµÄøÅĀŹ“óŌ¼ŹĒ![]() £¬³É¼ØøßÓŚ85·ÖµÄ“ĪŹżĪŖ
£¬³É¼ØøßÓŚ85·ÖµÄ“ĪŹżĪŖ![]() ·ž“Ó¶žĻī·Ö²¼£¬·Ö²¼ĮŠĪŖ
·ž“Ó¶žĻī·Ö²¼£¬·Ö²¼ĮŠĪŖ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() £¬
£¬ ![]()

 ŹżŃ§°ĀČüŹī¼ŁĢģĢģĮ·ÄĻ¾©“óѧ³ö°ęÉēĻµĮŠ“š°ø
ŹżŃ§°ĀČüŹī¼ŁĢģĢģĮ·ÄĻ¾©“óѧ³ö°ęÉēĻµĮŠ“š°ø ÄĻ“ó½ĢøØĒĄĻČĘšÅÜŹī¼ŁĻĪ½Ó½Ģ³ĢÄĻ¾©“óѧ³ö°ęÉēĻµĮŠ“š°ø
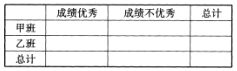
ÄĻ“ó½ĢøØĒĄĻČĘšÅÜŹī¼ŁĻĪ½Ó½Ģ³ĢÄĻ¾©“óѧ³ö°ęÉēĻµĮŠ“š°ø”¾ĢāÄæ”æĪ¢ŠÅŹĒĢŚŃ¶¹«Ė¾ĶĘ³öµÄŅ»ÖÖŹÖ»śĶØѶČķ¼ž£¬ĖüÖ§³Ö·¢ĖĶÓļŅō¶ĢŠÅ”¢ŹÓʵ”¢Ķ¼Ę¬ŗĶĪÄ×Ö£¬Ņ»¾ĶĘ³ö±ć·ēĆŅČ«¹ś£¬ÉõÖĮÓæĻÖ³öŅ»ÅśŌŚĪ¢ŠÅµÄÅóÓŃȦČĻśŹŪÉĢĘ·µÄČĖ£Ø±»³ĘĪŖĪ¢ÉĢ£©£®ĪŖĮĖµ÷²éĆæĢģĪ¢ŠÅÓĆ»§Ź¹ÓĆĪ¢ŠÅµÄŹ±¼ä£¬Ä³¾Ļś»ÆױʷµÄĪ¢ÉĢŌŚŅ»¹ć³”Ė껜²É·ĆÄŠŠŌ”¢Å®ŠŌÓĆ»§ø÷50 Ćū£¬ĘäÖŠĆæĢģĶęĪ¢ŠÅ³¬¹ż6 Š”Ź±µÄÓĆ»§ĮŠĪŖ”°Ī¢ŠÅæŲ”±£¬·ńŌņ³ĘĘäĪŖ”°·ĒĪ¢ŠÅæŲ”±£¬µ÷²é½į¹ūČēĻĀ£ŗ
Ī¢ŠÅæŲ | ·ĒĪ¢ŠÅæŲ | ŗĻ¼Ę | |
ÄŠŠŌ | 26 | 24 | 50 |
Å®ŠŌ | 30 | 20 | 50 |
ŗĻ¼Ę | 56 | 44 | 100 |
£Ø1£©øł¾ŻŅŌÉĻŹż¾Ż£¬ÄÜ·ńÓŠ60%µÄ°ŃĪÕČĻĪŖ”°Ī¢ŠÅæŲ”±Óė”±ŠŌ±š”°ÓŠ¹Ų£æ
£Ø2£©ĻÖ“Óµ÷²éµÄÅ®ŠŌÓĆ»§ÖŠ°“·Ö²ć³éŃłµÄ·½·ØŃ”³ö5 ČĖ²¢“ÓŃ”³öµÄ5 ČĖÖŠŌŁĖ껜³éČ”3 ČĖŌłĖĶ200 ŌŖµÄ»¤·ōĘ·Ģ××°£¬¼ĒÕā3 ČĖÖŠ”°Ī¢ŠÅæŲ”±µÄČĖŹżĪŖX£¬ŹŌĒóX µÄ·Ö²¼ĮŠÓėŹżŃ§ĘŚĶū£®
²Īæ¼¹«Ź½£ŗ![]() £¬ĘäÖŠn=a+b+c+d£®
£¬ĘäÖŠn=a+b+c+d£®
P£ØK2”Żk0£© | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
k0 | 0.455 | 0.708 | 1.323 | 3.841 | 5.024 | 6.635 |