题目内容
【题目】已知函数f(x)的定义域为(﹣1,1),对任意x,y∈(﹣1,1),有f(x)+f(y)=f( ![]() ).且当x<0时,f(x)>0.
).且当x<0时,f(x)>0.
(1)验证函数f(x)=lg ![]() 是否满足这些条件;
是否满足这些条件;
(2)若f( ![]() )=1,f(
)=1,f( ![]() )=2,且|a|<1,|b|<1,求f(a),f(b)的值.
)=2,且|a|<1,|b|<1,求f(a),f(b)的值.
(3)若f(﹣ ![]() )=1,试解关于x的方程f(x)=﹣
)=1,试解关于x的方程f(x)=﹣ ![]() .
.
【答案】
(1)解:由 ![]() 可得﹣1<x<1,即其定义域为(﹣1,1)
可得﹣1<x<1,即其定义域为(﹣1,1)
又 ![]() =
= 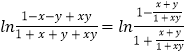 =
= ![]()
又当x<0时,1﹣x>1+x>0,∴ ![]() ∴
∴ ![]()
故 ![]() 满足这些条件
满足这些条件
(2)解:令x=y=0,∴f(0)=0,
令y=﹣x,有f(﹣x)+f(x)=f(0)=0,∴f(x)为奇函数
由条件得 ![]() ,解得
,解得 ![]()
(3)解:设﹣1<x1<x2<1,则x1﹣x2<0,1﹣x1x2>0, ![]() ,
,
则 ![]() ,f(x1)﹣f(x2)>0,∴f(x)在(﹣1,1)上是减函数
,f(x1)﹣f(x2)>0,∴f(x)在(﹣1,1)上是减函数
∵ ![]()
原方程即为 ![]() ,
,
∴ ![]()
又∵ ![]()
故原方程的解为 ![]()
【解析】(1)先求定义域看其是否满足条件,然后验证函数是否满足 ![]() ,最后求出当x<0时的值域,看是否满足即可;(2)先判定函数的奇偶性,然后
,最后求出当x<0时的值域,看是否满足即可;(2)先判定函数的奇偶性,然后 ![]() 建立f(a),f(b)的方程组,解之即可;(3)先判定函数f(x)在(﹣1,1)上的单调性,然后得到
建立f(a),f(b)的方程组,解之即可;(3)先判定函数f(x)在(﹣1,1)上的单调性,然后得到 ![]() ,建立关于x的方程,解之即可.
,建立关于x的方程,解之即可.
【考点精析】关于本题考查的函数的值,需要了解函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法才能得出正确答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目