题目内容
【题目】如图，在多面体ABCDEF中，DE⊥平面ABCD，AD∥BC，平面BCEF∩平面ADEF=EF，∠BAD=60°，AB=AD=2，DE=1．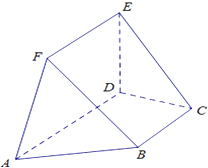 
（1）求证：BC∥EF；
（2）求三棱锥B﹣ADE的体积．
【答案】
（1）证明：∵AD∥BC，AD平面ADEF，BC平面ADEF
∴BC∥平面ADEF
又BC平面BCEF，平面BCEF∩平面ADEF=EF
∴BC∥EF
（2）解：∵DE⊥平面ABCD，∴DE是三棱锥E﹣ADB的高
又∠BAD=60°，AB=AD=2，∴三角形ADB是等边三角形
∴VB﹣ADE=VE﹣ADB= 
【解析】（1）由AD∥BC，得BC∥平面ADEF，由此能证明BC∥EF．（2）利用等体积转化求出三棱锥B﹣ADE的体积．
【考点精析】认真审题，首先需要了解空间中直线与直线之间的位置关系(相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点)．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】已知某中学高三文科班学生共有
人参加了数学与地理的水平测试，现学校决定利用随机数表法从中抽取
人进行成绩抽样统计，先将
人按
进行编号．
（Ⅰ）如果从第
行第
列的数开始向右读，请你依次写出最先检测的
个人的编号；（下面摘取了第
行 至第
行）
（Ⅱ）抽的
人的数学与地理的水平测试成绩如下表：
人数 | 数学 | |||
优秀 | 良好 | 及格 | ||
地 理 | 优秀 | 7 | 20 | 5 |
良好 | 9 | 18 | 6 | |
及格 |
| 4 |
| |
成绩分为优秀、良好、及格三个等级，横向、纵向分别表示地理成绩与数学成绩，例如：表中数学成绩为良好的共有
人，若在该样本中，数学成绩优秀率为
，求
的值．
（Ⅲ）将
的
表示成有序数对
，求“在地理成绩为及格的学生中，数学成绩为优秀的人数比及格的人数少”的数对
的概率．
