题目内容
【题目】已知抛物线G的顶点在原点,焦点在y轴正半轴上,点P(m,4)到其准线的距离等于5.
(1)求抛物线G的方程;
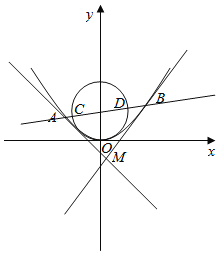
(2)如图,过抛物线G的焦点的直线依次与抛物线G及圆x2+(y﹣1)2=1交于A、C、D、B四点,试证明|AC||BD|为定值;
(3)过A、B分别作抛物G的切线l1,l2且l1,l2交于点M,试求△ACM与△BDM面积之和的最小值.
【答案】(1)x2=4y;(2)详见解析;(3)2.
【解析】
(1)利用抛物线的焦半径公式求P;(2)设直线AB方y=kx+1,与抛物线联立消去![]() ,结合焦半径公式化简从而得到定值;(3)欲求面积之和的最小值,利用直线AB的斜率作为自变量,建立函数模型,转化成求函数的最值问题.
,结合焦半径公式化简从而得到定值;(3)欲求面积之和的最小值,利用直线AB的斜率作为自变量,建立函数模型,转化成求函数的最值问题.
(1)由题知,抛物线的准线方程为y+1=0,故![]() 1
1
所以抛物线C的方程为x2=4y.
(2)当直线AB的斜率不存在时,直线与抛物线只有一个交点,
故直线AB的斜率一定存在,
设直线AB方y=kx+1交抛物线C于点A(x1,y1),B(x2,y2),
由抛物线定义知|AF|=y1+1,|BF|=y2+1,
所以|AC|=y1,|BD|=y2,
由 得x2﹣4kx﹣4=0,
得x2﹣4kx﹣4=0,
显然△>0,则x1+x2=4k,x1x2=﹣4,
所以y1y2![]() 1,所以|AC||BD|为定值1.
1,所以|AC||BD|为定值1.
(3)由x2=4y,y![]() x2,
x2, ![]() x,
x,
得直线AM方程y![]() x1(x﹣x1)(1),
x1(x﹣x1)(1),
直线BM方程y![]() x2(x﹣x2)(2),
x2(x﹣x2)(2),
由(2)﹣(1)得![]() (x1﹣x2)x
(x1﹣x2)x![]() ,
,
所以x![]() (x1+x2)=2k,∴y=﹣1
(x1+x2)=2k,∴y=﹣1
所以点M坐标为(2k,﹣1),
点M到直线AB距离d![]() 2
2![]() ,
,
弦AB长为|AB|![]() 4(1+k2),
4(1+k2),
△ACM与△BDM面积之和,
S![]() (|AB|﹣2)d
(|AB|﹣2)d![]() (2+4k2)×2
(2+4k2)×2![]() 2(1+2k2)
2(1+2k2)![]() ,
,
当k=0时,即AB方程为y=1时,△ACM与△BDM面积之和最小值为2.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案