题目内容
【题目】某旅游胜地欲开发一座景观山，从山的侧面进行勘测，迎面山坡线
由同一平面的两段抛物线组成，其中
所在的抛物线以
为顶点、开口向下，
所在的抛物线以
为顶点、开口向上，以过山脚（点）的水平线为
轴，过山顶（点）的铅垂线为
轴建立平面直角坐标系如图（单位：百米）．已知所在抛物线的解析式
，所在抛物线的解析式为
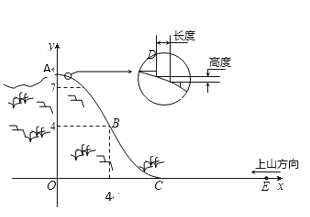
（1）求
值，并写出山坡线的函数解析式；
（2）在山坡上的700米高度（点
）处恰好有一小块平地，可以用来建造索道站，索道的起点选择在山脚水平线上的点
处，
（米），假设索道
可近似地看成一段以为顶点、开口向上的抛物线
当索道在上方时，索道的悬空高度有最大值，试求索道的最大悬空高度；
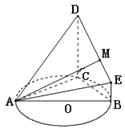
（3）为了便于旅游观景，拟从山顶开始、沿迎面山坡往山下铺设观景台阶，台阶每级的高度为20厘米，长度因坡度的大小而定，但不得少于20厘米，每级台阶的两端点在坡面上（见图）．试求出前三级台阶的长度（精确到厘米），并判断这种台阶能否一直铺到山脚，简述理由？
【答案】（1）
（2）
米 （3）第一级台阶的长度为
厘米，第二级台阶的长度为
厘米，第三级台阶的长度为
厘米，这种台阶不能从山顶一直铺到山脚.
【解析】
（1）将点点B（4,4）分别代入
，
求出
即可求得函数
的解析式；
（2）由已知有索道在
上方时，悬空高度
利用配方法可得
=
，再求最大值即可；
（3）由（1）得，在山坡线
上，
，
，
取
，
分别求出
，
再运算可得各级台阶的长度，再取点
，又取
，
运算可得
，即这种台阶不能一直铺到山脚，得解.
解：（1）将点B（4,4）分别代入，
解得
，
故；
（2）由图可知：
，由图观察可得：只有当索道在上方时，索道的悬空高度才有可能取最大值，
索道在上方时，悬空高度=
=，
当
时，
，
故索道的最大悬空高度为米；
(3)在山坡线上，，，
①令得
令
，得
，
所以第一级台阶的长度为
（百米）
（厘米），
同理，令得
所以第一级台阶的长度为（百米）（厘米），
所以第二级台阶的长度为
（百米）
（厘米），
所以第三级台阶的长度为
（百米）
（厘米），
②取点，又取，
则
，
因为，
故这种台阶不能从山顶一直铺到点
，从而就不能一直铺到山脚.
【题目】近年来，某市为促进生活垃圾的分类处理，将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类，并分别设置了相应的垃圾箱．为调查居民生活垃圾分类投放情况，现随机抽取了该市三类垃圾箱中总计1000t生活垃圾．经分拣以后数据统计如下表（单位：
）：根据样本估计本市生活垃圾投放情况，下列说法错误的是（ ）
厨余垃圾”箱 | 可回收物”箱 | 其他垃圾”箱 | |
厨余垃圾 | 400 | 100 | 100 |
可回收物 | 30 | 240 | 30 |
其他垃圾 | 20 | 20 | 60 |
A.厨余垃圾投放正确的概率为
B.居民生活垃圾投放错误的概率为
C.该市三类垃圾箱中投放正确的概率最高的是“可回收物”箱
D.厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量的方差为20000