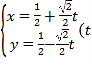题目内容
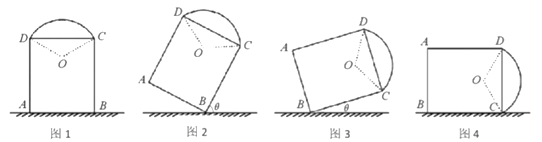
【题目】如图1,一艺术拱门由两部分组成,下部为矩形![]() 的长分别为
的长分别为![]() 米和
米和![]() 米,上部是圆心为
米,上部是圆心为![]() 的劣弧
的劣弧![]() ,
,![]()
(1)求图1中拱门最高点到地面的距离:
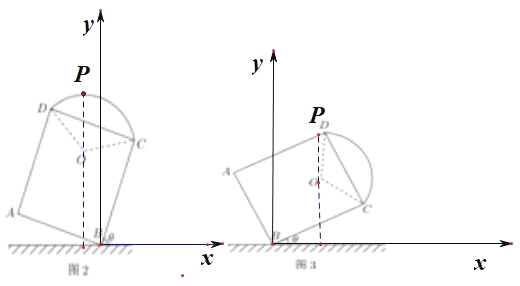
(2)现欲以![]() 点为支点将拱门放倒,放倒过程中矩形
点为支点将拱门放倒,放倒过程中矩形![]() 所在的平面始终与地面垂直,如图2、图3、图4所示,设
所在的平面始终与地面垂直,如图2、图3、图4所示,设![]() 与地面水平线
与地面水平线![]() 所成的角为
所成的角为![]() .若拱门上的点到地面的最大距离恰好为
.若拱门上的点到地面的最大距离恰好为![]() 到地面的距离,试求
到地面的距离,试求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据![]() 及
及![]() ,可求得圆的半径,根据最高点与圆心的关系即可求得到地面的距离.
,可求得圆的半径,根据最高点与圆心的关系即可求得到地面的距离.
(2)通过讨论P点所在的位置以及三角函数的性质可判断出h取最大值时θ取值范围.
(1)过O点作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,交
,交![]() 于
于![]() .如下图所示:
.如下图所示:
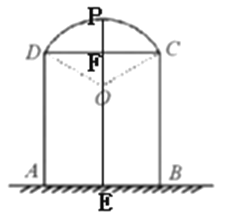
则![]() 即为所求.
即为所求.
因为![]() ,
,![]()
所以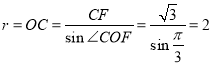
则![]()
所以![]()
即拱门最高点到地面的距离为5米
(2)在拱门放倒过程中,过点O作与地面垂直的直线与“拱门外框上沿”相交于点P.
当点P在劣弧CD上时,拱门上的点到地面的最大距离h等于圆O的半径长与圆心O到地面距离之和;
当点P在线段AD上时,拱门上的点到地面的最大距离h等于点D到地面的距离.
由(1)知,在Rt△OO1B中,OB![]() 2
2![]() .
.
以B为坐标原点,直线l为x轴,建立如图所示的坐标系.
①当点P在劣弧CD上时,![]() .
.
由∠OBx=θ![]() ,OB=2
,OB=2 ![]() ,
,
由三角函数定义,得O(2![]() cos(
cos(![]() ),2
),2![]() ),
),
则h=2+2![]() ,所以当θ
,所以当θ![]() 即θ
即θ![]() 时,h取得最大值2+2
时,h取得最大值2+2![]() ,
,
②当点P在线段AD上时,0≤θ![]() .
.
设∠CBD=φ,在Rt△BCD中,DB![]() 2
2![]() ,sinφ
,sinφ![]() ,cosφ
,cosφ![]() .
.
由∠DBx=θ+φ,得D(2![]() (θ+φ),2
(θ+φ),2![]() (θ+φ)).
(θ+φ)).
所以h=2![]() (θ+φ)=4sinθ+2
(θ+φ)=4sinθ+2![]() cosθ,
cosθ,
又当0<θ![]() 时,h′=4cosθ﹣2
时,h′=4cosθ﹣2![]() sinθ>4cos
sinθ>4cos![]() 2
2![]() sin
sin ![]() 0,
0,
所以h=4sinθ+2![]() 在[0,
在[0,![]() ]上递增.
]上递增.
所以当θ![]() 时,h取得最大值5.
时,h取得最大值5.
因为2+2![]() 5,所以h的最大值为2+2
5,所以h的最大值为2+2![]() .
.
综上,若拱门上的点到地面的最大距离恰好为D到地面的距离,则θ![]() .
.

 名校课堂系列答案
名校课堂系列答案